题目内容
如图，若正方形EFGH由正方形ABCD绕某点旋转得到，则可以作为旋转中心的是
- A.M或O或N
- B.E或O或C
- C.E或O或N
- D.M或O或C
A
分析：分类：若以M为旋转中心，把正方形ABCD顺时针旋转90°；若以O为旋转中心，把正方形ABCD旋转180°；若以N为旋转中心，把正方形ABCD逆时针旋转90°，然后通过分别找出正方形EFGH与正方形ABCD的对应点来判断正方形EFGH是否由正方形ABCD绕某点旋转得到．
解答：若以M为旋转中心，把正方形ABCD顺时针旋转90°，A点对应点为H，B点对应点为E，C点对应点为F，D点对应点为G，则可得到正方形EFGH；
若以O为旋转中心，把正方形ABCD旋转180°，A点对应点为G，B点对应点为H，C点对应点为E，D点对应点为F，则可得到正方形EFGH；
若以N为旋转中心，把正方形ABCD逆时针旋转90°，A点对应点为F，B点对应点为G，C点对应点为H，D点对应点为E，则可得到正方形EFGH．
故选A．
点评：本题考查了性质的性质：旋转前后两图形全等，即对应角相等，对应线段相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了正方形的性质．
分析：分类：若以M为旋转中心，把正方形ABCD顺时针旋转90°；若以O为旋转中心，把正方形ABCD旋转180°；若以N为旋转中心，把正方形ABCD逆时针旋转90°，然后通过分别找出正方形EFGH与正方形ABCD的对应点来判断正方形EFGH是否由正方形ABCD绕某点旋转得到．
解答：若以M为旋转中心，把正方形ABCD顺时针旋转90°，A点对应点为H，B点对应点为E，C点对应点为F，D点对应点为G，则可得到正方形EFGH；
若以O为旋转中心，把正方形ABCD旋转180°，A点对应点为G，B点对应点为H，C点对应点为E，D点对应点为F，则可得到正方形EFGH；
若以N为旋转中心，把正方形ABCD逆时针旋转90°，A点对应点为F，B点对应点为G，C点对应点为H，D点对应点为E，则可得到正方形EFGH．
故选A．
点评：本题考查了性质的性质：旋转前后两图形全等，即对应角相等，对应线段相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了正方形的性质．
练习册系列答案
相关题目
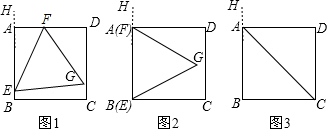
如图1，正方形ABCD和正三角形EFG的边长都为1，点E，F分别在线段AB，AD上滑动，设点G到CD的距离为x，到BC的距离为y，记∠HEF为α（当点E，F分别与B，A重合时，记α=0°）．
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
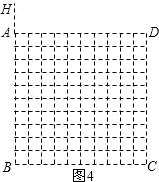
（4）若将“点E，F分别在线段AB，AD上滑动”改为“点E，F分别在正方形ABCD边上滑动”．当滑动一周时，请使用（3）的结果，在图4中描出部分点后，勾画出点G运动所形成的大致图形．
（参考数据：
≈1.732，sin15°=
≈0.259，sin75°=
≈0.966）
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
| α | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| x | 0.03 | 0 | 0.29 | ||||
| y | 0.29 | 0.13 | 0.03 |
（参考数据：
| 3 |
| ||||
| 4 |
| ||||
| 4 |
如图1，正方形ABCD和正三角形EFG的边长都为1，点E，F分别在线段AB，AD上滑动，设点G到CD的距离为x，到BC的距离为y，记∠HEF为 （当点E，F分别与B，A重合时，记 ）． | ||||||||||||||||||||||||
 | ||||||||||||||||||||||||
（1）当 时（如图2所示），求x，y的值（结果保留根号）；（2）当  为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；（3）请你补充完成下表（精确到0.01）： | ||||||||||||||||||||||||
（参考数据：  ） |
如图1，正方形ABCD和正三角形EFG的边长都为1，点E，F分别在线段AB，AD上滑动，设点G到CD的距离为x，到BC的距离为y，记∠HEF为α（当点E，F分别与B，A重合时，记α=0°）．
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
（4）若将“点E，F分别在线段AB，AD上滑动”改为“点E，F分别在正方形ABCD边上滑动”．当滑动一周时，请使用（3）的结果，在图4中描出部分点后，勾画出点G运动所形成的大致图形．
（参考数据：
≈1.732，sin15°=
≈0.259，sin75°=
≈0.966）
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
| α | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| x | 0.03 | 0.29 | |||||
| y | 0.29 | 0.13 | 0.03 |
（参考数据：
≈1.732，sin15°=≈0.259，sin75°=≈0.966）
如图1，正方形ABCD和正三角形EFG的边长都为1，点E，F分别在线段AB，AD上滑动，设点G到CD的距离为x，到BC的距离为y，记∠HEF为α（当点E，F分别与B，A重合时，记α=0°）．
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
（4）若将“点E，F分别在线段AB，AD上滑动”改为“点E，F分别在正方形ABCD边上滑动”．当滑动一周时，请使用（3）的结果，在图4中描出部分点后，勾画出点G运动所形成的大致图形．
（参考数据：
≈1.732，sin15°=
≈0.259，sin75°=
≈0.966）
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
| α | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| x | 0.03 | 0.29 | |||||
| y | 0.29 | 0.13 | 0.03 |
（参考数据：
≈1.732，sin15°=≈0.259，sin75°=≈0.966）
（2008•江西）如图1，正方形ABCD和正三角形EFG的边长都为1，点E，F分别在线段AB，AD上滑动，设点G到CD的距离为x，到BC的距离为y，记∠HEF为α（当点E，F分别与B，A重合时，记α=0°）．
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
（4）若将“点E，F分别在线段AB，AD上滑动”改为“点E，F分别在正方形ABCD边上滑动”．当滑动一周时，请使用（3）的结果，在图4中描出部分点后，勾画出点G运动所形成的大致图形．
（参考数据：
≈1.732，sin15°=
≈0.259，sin75°=
≈0.966）
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
| α | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| x | 0.03 | 0.29 | |||||
| y | 0.29 | 0.13 | 0.03 |
（参考数据：
≈1.732，sin15°=≈0.259，sin75°=≈0.966）