题目内容
 正比例函数y=x与反比例函数y=
正比例函数y=x与反比例函数y=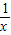 的图象相交于A、C两点.AB⊥x轴于B,CD⊥y轴于D(如图),则四边形ABCD的面积为( )
的图象相交于A、C两点.AB⊥x轴于B,CD⊥y轴于D(如图),则四边形ABCD的面积为( )A.1
B.

C.2
D.

【答案】分析:首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|,得出S△AOB=S△ODC=
|k|,得出S△AOB=S△ODC= ,再根据反比例函数的对称性可知:OB=OD,得出S△AOB=S△ODA,S△ODC=S△OBC,最后根据四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC,得出结果.
,再根据反比例函数的对称性可知:OB=OD,得出S△AOB=S△ODA,S△ODC=S△OBC,最后根据四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC,得出结果.
解答:解:根据反比例函数的对称性可知:OB=OD,AB=CD,
∴四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC=1×2=2.
故选C.
点评:本题主要考查了反比例函数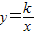 中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|.
|k|.
 |k|,得出S△AOB=S△ODC=
|k|,得出S△AOB=S△ODC= ,再根据反比例函数的对称性可知:OB=OD,得出S△AOB=S△ODA,S△ODC=S△OBC,最后根据四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC,得出结果.
,再根据反比例函数的对称性可知:OB=OD,得出S△AOB=S△ODA,S△ODC=S△OBC,最后根据四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC,得出结果.解答:解:根据反比例函数的对称性可知:OB=OD,AB=CD,
∴四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC=1×2=2.
故选C.
点评:本题主要考查了反比例函数
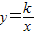 中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|.
|k|. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
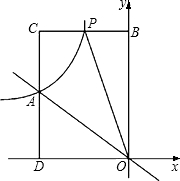 如图所示,正比例函数y=kx与反比例函数
如图所示,正比例函数y=kx与反比例函数 (2012•海南)如图,正比例函数y=k1x与反比例函数y=
(2012•海南)如图,正比例函数y=k1x与反比例函数y=