题目内容
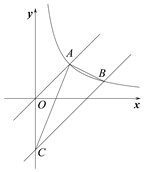
【题目】如图,在平面直角坐标系 xOy 中,点 A 是反比例函数 y=![]() 在第一象限的图象上一点,连接 AO,并以 AO 为直角边作 Rt△AOB,点 B 落在第二象限内,斜边 AB 交 y 轴于点 C.若 BC=2CA,tanA=
在第一象限的图象上一点,连接 AO,并以 AO 为直角边作 Rt△AOB,点 B 落在第二象限内,斜边 AB 交 y 轴于点 C.若 BC=2CA,tanA= ![]() ,则点 A 的坐标为_____.
,则点 A 的坐标为_____.

【答案】( ![]() ,
,![]() )
)
【解析】
作AM⊥x轴于M,BN⊥x轴于N.由BN∥OC∥AM,推出ON:OM=BC:AC=2,时ON=2a,则OM=a,AM=![]() ,由△BNO∽△OMA,可得
,由△BNO∽△OMA,可得![]() =tanA=
=tanA=![]() ,由此构建方程求出a即可解决问题;
,由此构建方程求出a即可解决问题;
作AM⊥x轴于M,BN⊥x轴于N.
∵BN∥OC∥AM,
∴ON:OM=BC:AC=2,时ON=2a,则OM=a,AM=![]() ,
,
∵∠ONB=∠AMO=∠AOB=90°,
∴∠BON+∠AOM=90°,∠AOM+∠MAO=90°,
∴∠BON=∠MAO,
∴△BNO∽△OMA,
∴![]() =tanA=
=tanA=![]() ,
,
∴![]() ,
,
∴a=![]() ,
,
∴A(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() ).
).

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目