题目内容
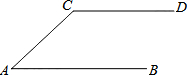 如图,AB∥CD,
如图,AB∥CD,(1)根据要求作图:①作∠CAB的平分线交CD于M;②作CN⊥AM于N.
(2)在(1)的条件下
①若∠ACD=114°,求∠MAB的度数;
②求证:△ACN≌△MCN.
考点:作图—复杂作图,全等三角形的判定
专题:
分析:(1)根据角平分线的作法作∠CAB的平分线交CD于M,再根据过直线外一点作已知直线的垂线的方法作图即可;
(2)①根据角平分线的性质可得∠CAD=∠DAC=
∠CAB,再根据平行线的性质可得∠C+∠CAB=180°,进而可得答案;
②根据垂线定义可得∠CNA=∠CNM=90°,然后再证明∠CAD=∠CDA,再加上公共边CN可利用AAS定理证明△ACN≌△MCN.
(2)①根据角平分线的性质可得∠CAD=∠DAC=
| 1 |
| 2 |
②根据垂线定义可得∠CNA=∠CNM=90°,然后再证明∠CAD=∠CDA,再加上公共边CN可利用AAS定理证明△ACN≌△MCN.
解答: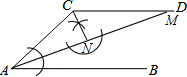 解:(1)如图所示:
解:(1)如图所示:
(2)①∵AM平分∠ACD,
∴∠CAD=∠DAC=
∠CAB,
∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠ACD=114°,
∴∠CAD=66°,
∴∠MAB=33°;
②∵CN⊥AM,
∴∠CNA=∠CNM=90°,
∵AB∥CD,
∴∠ADC=∠DAB,
∴∠CAD=∠CDA,
在△ACN和△DCN中
,
∴△ACN≌△MCN(AAS).
 解:(1)如图所示:
解:(1)如图所示:(2)①∵AM平分∠ACD,
∴∠CAD=∠DAC=
| 1 |
| 2 |
∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠ACD=114°,
∴∠CAD=66°,
∴∠MAB=33°;
②∵CN⊥AM,
∴∠CNA=∠CNM=90°,
∵AB∥CD,
∴∠ADC=∠DAB,
∴∠CAD=∠CDA,
在△ACN和△DCN中
|
∴△ACN≌△MCN(AAS).
点评:此题主要考查了复杂作图,以及角平分线的性质,平行线的性质和全等三角形的判定,关键是正确作出图形.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
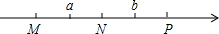 如图,M,N,P分别是数轴上三个整数对应的点,且MN=NP=1,数a对应的点在M与N之间,数b对应的点在N和P之间,若|a|+|b|=2,则在M、N、P三个点中,原点不可能是( )
如图,M,N,P分别是数轴上三个整数对应的点,且MN=NP=1,数a对应的点在M与N之间,数b对应的点在N和P之间,若|a|+|b|=2,则在M、N、P三个点中,原点不可能是( )| A、M | B、N | C、P | D、M或P |
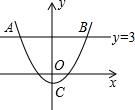 如图,抛物线y=ax2+c与直线y=3相交于A、B,点A的横坐标为-4,与y轴相交于点C(0,-1),从图象可知,当0≤ax2+c≤3时,自变量x的取值范围是( )
如图,抛物线y=ax2+c与直线y=3相交于A、B,点A的横坐标为-4,与y轴相交于点C(0,-1),从图象可知,当0≤ax2+c≤3时,自变量x的取值范围是( )| A、-4≤x≤3 |
| B、-4≤x≤-2或2≤x≤4 |
| C、-4≤x≤4 |
| D、x≤-2或x≥2 |
 某船在大海上行到O处,沿北偏东60°方向航行2海里后,再沿北偏西30°方向航行2海里,以下面线段AB为一海里,在下图上画同航线.
某船在大海上行到O处,沿北偏东60°方向航行2海里后,再沿北偏西30°方向航行2海里,以下面线段AB为一海里,在下图上画同航线. 已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到,这时图象与x轴的交点为A、B(A在B的左边),与y轴交于点C.
已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到,这时图象与x轴的交点为A、B(A在B的左边),与y轴交于点C. 如图,是一个长方形鸡场的平面示意图,一边靠墙,另外三面用篱笆围成.若篱笆总长为35m,所围的面积为150m2,求长方形鸡场的长和宽.
如图,是一个长方形鸡场的平面示意图,一边靠墙,另外三面用篱笆围成.若篱笆总长为35m,所围的面积为150m2,求长方形鸡场的长和宽. 看图填空:
看图填空: 如图所示,矩形ABCD中,AB=4,AD=
如图所示,矩形ABCD中,AB=4,AD=