题目内容
已知:关于 的一元二次方程
的一元二次方程 .
.
(1)求实数k的取值范围;
(2)设上述方程的两个实数根分别为x1、x2,求:当 取哪些整数时,x1、x2均为整数;
取哪些整数时,x1、x2均为整数;
(3)设上述方程的两个实数根分别为x1、x2,若 ,求k的值.
,求k的值.
 的一元二次方程
的一元二次方程 .
.(1)求实数k的取值范围;
(2)设上述方程的两个实数根分别为x1、x2,求:当
 取哪些整数时,x1、x2均为整数;
取哪些整数时,x1、x2均为整数;(3)设上述方程的两个实数根分别为x1、x2,若
 ,求k的值.
,求k的值.(1)k≠0;(2)k=±1或者k=±2;(3)  .
.
 .
.试题分析:(1)一元二次方程存在的条件是二次项系数不为零,根据题意,kx2+2x+2-k=0是关于x的一元二次方程,所以k≠0;(2)根据求根公式,可以将方程的解求出来,
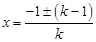 ,
, ,
,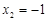 ,要使得方程的根为整数,只要要求
,要使得方程的根为整数,只要要求 是整数即可,进而只要要求
是整数即可,进而只要要求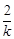 为整数,k是2的因数,所以k=±1或者k=±2;(3)方法一:由(2)可以得到
为整数,k是2的因数,所以k=±1或者k=±2;(3)方法一:由(2)可以得到  ,
,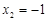 ,所以
,所以 ,分类讨论,①当
,分类讨论,①当 时,此方程无解;②当
时,此方程无解;②当 时,解得
时,解得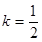 ;方法二:可以根据根与系数关系
;方法二:可以根据根与系数关系 ,
, 进行求解,具体详见解析.
进行求解,具体详见解析.试题解析:(1) ∵方程
 是关于x的一元二次方程,
是关于x的一元二次方程,∴实数k的取值范围是k≠0.
(2)△= b2-4ac=4-4k(2-k)=k2-2k+1=(k-1)2 ,
由求根公式,得
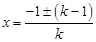 ,
,∴
 ,
,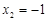 ,
,∵要求两个实数根x1、x2是整数,
∴
 为整数,即
为整数,即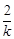 是整数,
是整数,∴k是2的因数, k=±1或者k=±2.
(3)方法一:由(2)可以得到
 ,
,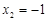 ,
,∴
 ,分类讨论:
,分类讨论:①当
 时,此方程无解;
时,此方程无解;②当
 时,解得
时,解得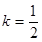 ;
;方法二:根据题意,
 ,两边平方,有
,两边平方,有 ,
,整理得
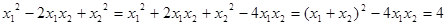 ,
,由根与系数的关系
 ,
, ,
, ∴
 ,
,整理,得8k-4=0,k=
 .
.
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 和
和 .
.
 .
. 的一次项是( )
的一次项是( )



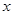 m,则根据题意可列方程为 __ .
m,则根据题意可列方程为 __ .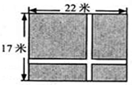
 = .
= . ,且一元二次方程
,且一元二次方程 有实数根,则
有实数根,则 的取值范围
的取值范围