题目内容
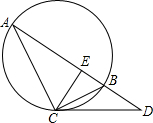 如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=
如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD= ,则AC的长为
,则AC的长为
- A.
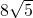
- B.

- C.10
- D.
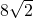
A
分析:连结OC,在Rt△DCE中利用cosD=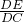 =
= ,可设DE=4x,则DC=5x,于是CE=3x=8,解得x=
,可设DE=4x,则DC=5x,于是CE=3x=8,解得x= 得到DE=
得到DE= ,DC=
,DC= ,根据圆周角定理AB为直径得到∠ACB=90°,利用∠A=∠BCD可得到∠OCD=90°,在Rt△OCD中,根据cosD=
,根据圆周角定理AB为直径得到∠ACB=90°,利用∠A=∠BCD可得到∠OCD=90°,在Rt△OCD中,根据cosD= =
= =
= ,解得OD=
,解得OD= ,则OE=OD-DE=6,接着根据勾股定理计算出OC,然后再次利用勾股定理计算AC.
,则OE=OD-DE=6,接着根据勾股定理计算出OC,然后再次利用勾股定理计算AC.
解答:连结OC,如图,
∵CE⊥AB,
∴∠AEC=∠CED=90°,
∴cosD=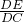 =
= ,
,
设DE=4x,则DC=5x,
∴CE=3x=8,解得x= ,
,
∴DE= ,DC=
,DC= ,
,
∵AB为直径,
∴∠ACB=90°,
∵∠A=∠BCD,
而∠A=∠ACO,
∴∠ACO=∠BCD,
∴∠OCD=90°,
在Rt△OCD中,cosD= =
= =
= ,解得OD=
,解得OD= ,
,
∴OE=OD-DE= -
- =6,
=6,
在Rt△OCE中,OC= =10,
=10,
∴OA=10,
∴AE=10+6=16,
在Rt△ACE中,AC= =
= =8
=8 .
.
故选A.
点评:本题考查了相似三角形的判定与性质:两组角对应相等的两个三角形相似;相似三角形对应边的比相等.也考查了圆周角定理和解直角三角形.
分析:连结OC,在Rt△DCE中利用cosD=
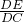 =
= ,可设DE=4x,则DC=5x,于是CE=3x=8,解得x=
,可设DE=4x,则DC=5x,于是CE=3x=8,解得x= 得到DE=
得到DE= ,DC=
,DC= ,根据圆周角定理AB为直径得到∠ACB=90°,利用∠A=∠BCD可得到∠OCD=90°,在Rt△OCD中,根据cosD=
,根据圆周角定理AB为直径得到∠ACB=90°,利用∠A=∠BCD可得到∠OCD=90°,在Rt△OCD中,根据cosD= =
= =
= ,解得OD=
,解得OD= ,则OE=OD-DE=6,接着根据勾股定理计算出OC,然后再次利用勾股定理计算AC.
,则OE=OD-DE=6,接着根据勾股定理计算出OC,然后再次利用勾股定理计算AC.解答:连结OC,如图,

∵CE⊥AB,
∴∠AEC=∠CED=90°,
∴cosD=
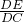 =
= ,
,设DE=4x,则DC=5x,
∴CE=3x=8,解得x=
 ,
,∴DE=
 ,DC=
,DC= ,
,∵AB为直径,
∴∠ACB=90°,
∵∠A=∠BCD,
而∠A=∠ACO,
∴∠ACO=∠BCD,
∴∠OCD=90°,
在Rt△OCD中,cosD=
 =
= =
= ,解得OD=
,解得OD= ,
,∴OE=OD-DE=
 -
- =6,
=6,在Rt△OCE中,OC=
 =10,
=10,∴OA=10,
∴AE=10+6=16,
在Rt△ACE中,AC=
 =
= =8
=8 .
.故选A.
点评:本题考查了相似三角形的判定与性质:两组角对应相等的两个三角形相似;相似三角形对应边的比相等.也考查了圆周角定理和解直角三角形.

练习册系列答案
相关题目
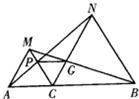 25、如图,已知点C在线段AB上,以AC和BC为边在AB同侧作正△ACM和正△BCN,连接AN,BM,分别交CM,CN于点P,G,连接PG.求证:PG∥AB.
25、如图,已知点C在线段AB上,以AC和BC为边在AB同侧作正△ACM和正△BCN,连接AN,BM,分别交CM,CN于点P,G,连接PG.求证:PG∥AB. 6、问题:“如图,已知点O在直线l上,以线段OD为一边画等腰三角形,且使另一顶点A在直线l上,则满足条件的A点有几个?”.我们可以用圆规探究,按如图的方式,画图找到4个点:A1、A2、A3、A4.这种问题说明的方式体现了( )的数学思想方法.
6、问题:“如图,已知点O在直线l上,以线段OD为一边画等腰三角形,且使另一顶点A在直线l上,则满足条件的A点有几个?”.我们可以用圆规探究,按如图的方式,画图找到4个点:A1、A2、A3、A4.这种问题说明的方式体现了( )的数学思想方法.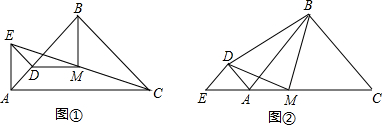
 如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=
如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=