题目内容
 已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OD.
已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OD.(1)求证:∠D=90°-2∠BAC;
(2)若EB=8cm,CD=24cm,求⊙O的直径.
考点:垂径定理,勾股定理
专题:
分析:(1)连接AD,OD,求得∠OAD=∠ODA,∠CAE=∠DAE,进而求得∠EOD=2∠OAD,即可求得∠ODE=90°-∠EOD=90°-2∠OAD=90°-2∠BAC.
(2)根据垂径定理得出ED=12cm,然后根据勾股定理即可求得⊙O的半径,进而求得直径.
(2)根据垂径定理得出ED=12cm,然后根据勾股定理即可求得⊙O的半径,进而求得直径.
解答: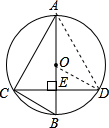 解:(1)连接AD,OD,
解:(1)连接AD,OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠EOD=∠OAD+∠ODA,
∴∠EOD=2∠OAD,
∵AB为⊙O的直径,CD是弦,且AB⊥CD于点E,
∴CE=DE,
∴AC=AD,
∴∠CAE=∠DAE,
∴∠ODE=90°-∠EOD=90°-2∠OAD=90°-2∠BAC.
(2)∵CD=24cm,EB=8cm,
∴ED=12cm,
在RT△OED中,OD=OB,
∵OD2=(OB-BE)2+DE2
设OD=OB=R
R2=(R-8)2+122
解得R=13,
∴2R=26,
∴⊙O的直径为26cm
 解:(1)连接AD,OD,
解:(1)连接AD,OD,∵OA=OD,
∴∠OAD=∠ODA,
∵∠EOD=∠OAD+∠ODA,
∴∠EOD=2∠OAD,
∵AB为⊙O的直径,CD是弦,且AB⊥CD于点E,
∴CE=DE,
∴AC=AD,
∴∠CAE=∠DAE,
∴∠ODE=90°-∠EOD=90°-2∠OAD=90°-2∠BAC.
(2)∵CD=24cm,EB=8cm,
∴ED=12cm,
在RT△OED中,OD=OB,
∵OD2=(OB-BE)2+DE2
设OD=OB=R
R2=(R-8)2+122
解得R=13,
∴2R=26,
∴⊙O的直径为26cm
点评:本题考查了垂径定理的应用,勾股定理的应用,三角形的外角的性质等,应用垂径定理得出AB垂直平分CD是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
| A、-1的相反数是-1 |
| B、-1的倒数是-1 |
| C、(-1)3=1 |
| D、-1的绝对值是-1 |
 一个简易的起重装置如图所示,其中a=12m,b=22m,a和b的夹角是120°,求c的长(保留根号).
一个简易的起重装置如图所示,其中a=12m,b=22m,a和b的夹角是120°,求c的长(保留根号).