题目内容
【题目】21.(2013年四川攀枝花8分)某文具店准备购进甲,乙两种铅笔,若购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元;
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案;
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大;最大利润是多少元.
【答案】(1)甲,乙两种钢笔每支各需5元和10元;(2)六种;(3)乙钢笔20支,甲钢笔160支时获利最大,最大利润为380元.
【解析】
(1)先设购进甲,乙两种钢笔每支各需a元和b元,根据购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元列出方程组,求出a,b的值即可.
(2)先设购进甲钢笔x支,乙钢笔y支,根据题意列出5x+10y=1000和不等式组6y≤x≤8y,把方程代入不等式组即可得出20≤y≤25,求出y的值即可.
(3)先设利润为W元,得出W=2x+3y=400﹣y,根据一次函数的性质求出最大值.
解:(1)设购进甲,乙两种钢笔每支各需a元和b元,根据题意得:
![]() ,解得:
,解得:![]() .,
.,
答:购进甲,乙两种钢笔每支各需5元和10元.
(2)设购进甲钢笔x支,乙钢笔y支,根据题意可得:
![]() ,解得:20≤y≤25.
,解得:20≤y≤25.
∵x,y为整数,∴y=20,21,22,23,24,25共六种方案.
∵5x=1000﹣10y>0,∴0<y<100.
∴该文具店共有6种进货方案.
(3)设利润为W元,则W=2x+3y,
∵5x+10y=1000,∴x=200﹣2y,代入上式得:W=400﹣y.
∵W随着y的增大而减小,
∴当y=20时,W有最大值,最大值为W=400﹣20=380(元).
即当乙钢笔20支,甲钢笔160支时获利最大,最大利润为380元.

【题目】将长为![]() ,宽为
,宽为![]() 的长方形白纸,按图示方法粘合起来,粘合部分宽为
的长方形白纸,按图示方法粘合起来,粘合部分宽为![]() .
.
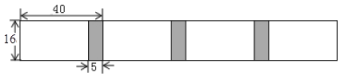
(1)根据图示,将下表补充完整;
白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
纸条长度/ | 40 | 110 | 145 | … |
(2)设![]() 张白纸粘合后的总长度为
张白纸粘合后的总长度为![]() ,求
,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)将若干张白纸按上述方式粘合起来,你认为总长度可能为![]() 吗?为什么?
吗?为什么?