题目内容
11.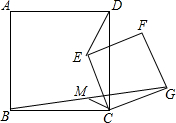 已知正方形ABCD和正方形CEFG共顶点于C.M是BG的中点.求证:CM⊥DE.
已知正方形ABCD和正方形CEFG共顶点于C.M是BG的中点.求证:CM⊥DE.
分析 如图,延长BC到P,使得CP=BC,连接PG,延长PG交CD于点O,交DE于点N.首先证明△PCG≌△DCE,∠P=∠CDE,推出PN⊥DE,再证明CM∥PN即可证明.
解答 解:如图,延长BC到P,使得CP=BC,连接PG,延长PG交CD于点O,交DE于点N.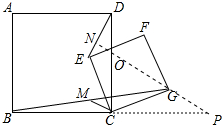
∵四边形ABCD,四边形EFGC都是正方形,
∴∠ECG=∠BCD=∠DCP=90°,BC=CD=CP,EC=CG,
在△GCP和△ECD中,
$\left\{\begin{array}{l}{CP=CD}\\{∠PCG=∠DCE}\\{CG=CE}\end{array}\right.$,
∴△PCG≌△DCE,
∴∠P=∠CDE,
∵∠P+∠POC=90°,∠POC=∠DON,
∴∠CDE+∠DON=90°,
∴∠DNO=90°,∴DE⊥PN,
∵BM=MG,BC=CP,
∴CM∥PN,
∴DE⊥CM.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.同时考查了正方形的性质和三角形全等的判定与性质以及三角形中位线定理等知识,解题的关键是PN⊥BD的证明,学会添加常用辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
相关题目
16.关于函数y=-2x,下列叙述正确是( )
| A. | 函数图象经过点(1,2) | B. | 函数图象经过第三、四象限 | ||
| C. | y随x的增大而减小 | D. | 不论x取何值,总有y<0 |
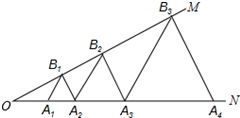 如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为32.
如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为32.