题目内容
阅读以下例题:“解不等式:(x+4)(x-1)>0
解:①当x+4>0,则x-1>0当若x+4<0,则x-1<0
即可以写成:
即可以写成:
解不等式组得:
解不等式组得:
综合以上两种情况:不等式解集:x>1或 x<-4
(以上解法依据:若ab>0,则a,b同号)请你模仿例题的解法,解不等式:
(1)(x-1)(x-2)>0;
(2)(x-2)(x-3)<0.
解:①当x+4>0,则x-1>0当若x+4<0,则x-1<0
即可以写成:
|
|
解不等式组得:
|
|
综合以上两种情况:不等式解集:x>1或 x<-4
(以上解法依据:若ab>0,则a,b同号)请你模仿例题的解法,解不等式:
(1)(x-1)(x-2)>0;
(2)(x-2)(x-3)<0.
分析:(1)根据例题可得:此题分两个不等式组
和
,分别解出两个不等式组即可;
(2)根据两数相乘,异号得负可得此题也分两种情况)①
,②
,解出不等式组即可.
|
|
(2)根据两数相乘,异号得负可得此题也分两种情况)①
|
|
解答:解:(1)①当x-1>0时,x-2>0,可以写成
;
解得:x>2;
②x-1<0时,x-2<0,可以写成
,
解得:x<1,
综合以上两种情况:不等式解集:x>2或 x<1;
(2)①x-2>0时,x-3<0,
可以写成
,
解得2<x<3;
②x-2<0时,x-3>0,
可以写成
,
解得:无解,
综合以上两种情况:不等式解集:2<x<3.
|
解得:x>2;
②x-1<0时,x-2<0,可以写成
|
解得:x<1,
综合以上两种情况:不等式解集:x>2或 x<1;
(2)①x-2>0时,x-3<0,
可以写成
|
解得2<x<3;
②x-2<0时,x-3>0,
可以写成
|
解得:无解,
综合以上两种情况:不等式解集:2<x<3.
点评:此题主要考查了不等式的解法,关键是正确理解例题的解题根据,然后再进行计算.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 ,则
,则 当若
当若 ,则
,则
 即可以写成:
即可以写成:
 解不等式组得:
解不等式组得:
 或
或 
 ,则
,则 同号)请你模仿例题的解法,解不等式:
同号)请你模仿例题的解法,解不等式: (2)
(2)
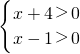 即可以写成:
即可以写成: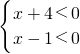
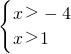 解不等式组得:
解不等式组得: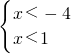

 ,则
,则 当若
当若 ,则
,则
 即可以写成:
即可以写成:
 解不等式组得:
解不等式组得:
 或
或 
 ,则
,则 同号)请你模仿例题的解法,解不等式:
同号)请你模仿例题的解法,解不等式: (2)
(2)