题目内容
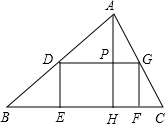
 如图,O是矩形ABCD对角线的交点,作BE∥AC,CE∥BD,BE、CE交于点E.
如图,O是矩形ABCD对角线的交点,作BE∥AC,CE∥BD,BE、CE交于点E.
(1)四边形OBEC是菱形吗?说说你的理由;
(2)若BC=8,AB=6,求四边形OBEC的周长和面积.
 解:(1)是,
解:(1)是,证明:∵四边形ABCD是矩形,
∴BO=CO,
∵BE∥AC,CE∥BD,
∴四边形BECO是平行四边形,
∴四边形OBEC是菱形.
(2)∵BC=8,AB=6,
∴AC=
 =10,
=10,∴CO=
 AC=5,
AC=5,∴菱形周长=20,
∵四边形OBEC是菱形,
∴CF=
 BC=4,OE⊥BC,
BC=4,OE⊥BC,∴OF=
 =3,
=3,∴OE=6,
∴菱形的面积=6×8÷2=24.
分析:(1)首先根据条件BE∥AC,CE∥BD可证出四边形BECO是平行四边形,再根据矩形的性质得到BO=CO,即可得到四边形OBEC是菱形;
(2)首先利用勾股定理求出AC的长,再根据矩形的性质得到CO的长,再根据菱形的性质得到周长;利用勾股定理求出OE的一半长,根据菱形的面积公式=对角线长×
 即可得到答案.
即可得到答案.点评:此题主要考查了矩形的性质,勾股定理的应用,菱形的判定与性质,解决题目的关键是熟练掌握矩形与菱形性质的区别与联系.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目

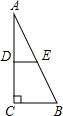 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )