题目内容
【题目】平行四边形ABCD在平面直角坐标系中的位置如图所示，已知AB=8，AD=6，∠BAD=60°，点A的坐标为（-2，0）．
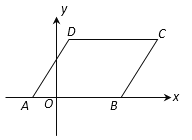
求：（1）点C的坐标；
（2）直线AC与y轴的交点E的坐标．
【答案】（1）C(9， 
)；（2）E（0，
）
【解析】
(1)过C作CH⊥x轴于点H,利用平行四边形的性质结合直角三角形的性质得出C点坐标;
(2) 利用待定系数法求出一次函数解析式，再利用x =0进而得出答案．
解：（1）过C作CH⊥x轴于点H，
∵四边形ABCD为平行四边形，
∴CD=AB=8，BC=AD=6，AB//DC，AD//BC．
∴∠BAD=∠HBC
∵∠BAD =60°，
∴∠HBC=60°．
∴BH=3，CH=．
∵A（-2，0），
∴AO=2．
∴OB=6．
∴OH=OB+BH=9．
∴C(9，)．
（2）设直线AC的表达式为：y=kx+b，把A（-2，0）和C(9，)代入，得
∴
，
解得：
∴
．
∴E（0，）
练习册系列答案
相关题目
【题目】某商店新进一种台灯．这种台灯的成本价为每个30元，经调查发现，这种台灯每天的销售量y（单位：个）是销售单价x（单位：元）（30≤x≤60）的一次函数．
x | 30 | 35 | 40 | 45 | 50 |
y | 30 | 25 | 20 | 15 | 10 |
（1）求销售量y与销售单价x之间的函数表达式；
（2）设这种台灯每天的销售利润为w元．这种台灯销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？
