题目内容

△ABC的边长AB=2，面积为1，直线PQ∥BC，分别交AB、AC于P、Q，设AP=t，△APQ面积为S，则S关于t的函数图象大致是（　　）
分析：根据题意，由相似三角形的判定，易∴△APQ∽△ABC，由相似三角形的性质，可得S与t的关系，进而分析选项可得答案．
解答：解：根据题意，∵PQ∥BC，
∴△APQ∽△ABC，
∴（
AP
AB
）2=
S
2
，
∴（
t
2
）2=
S
2
，
∴S=
1
2
t2，0≤t≤2，
结合二次函数的图象，可得其图象为B．
故选：B．
点评：本题考查二次函数的图象的确定方法，要求学生根据题意，得出其解析式，进而得到图象．
练习册系列答案
相关题目
等腰直角△ABC和⊙O如图放置，已知AB=BC=1，∠ABC=90°，⊙O的半径为1，圆心O与直线AB的距离为5．现△ABC以每秒2个单位的速度向右移动，同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大．
（1）当△ABC的边（BC边除外）与圆第一次相切时，点B移动了多少距离？
（2）若在△ABC移动的同时，⊙O也以每秒1个单位的速度向右移动，则△ABC从开始移动，到它的边与圆最后一次相切，一共经过了多少时间？
（3）在（2）的条件下，是否存在某一时刻，△ABC与⊙O的公共部分等于⊙O的面积？若存在，求出恰好符合条件时两个图形移动了多少时间？若不存在，请说明理由．
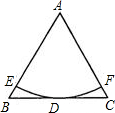精英家教网
精英家教网如图，正△ABC的边长AB=2，以A为圆心的圆切BC于点D，交AB于点E，交AC于点F，则弧EF的长=
 
．
等腰直角△ABC和⊙O如图放置，已知AB=BC=1，∠ABC=90°，⊙O的半径为1，圆心O与直线AB的距离为5．现两个图形同时向右移动，△ABC的速度为每秒2个单位，⊙O的速度为每秒1个单位，同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大．

（1）△ABC的边与圆第一次相切时，点B运动了多少距离？
（2）从△ABC的边与圆第一次相切到最后一次相切，共经过多少时间？
（3）是否存在某一时刻，△ABC与⊙O的公共部分等于⊙O的面积？若存在，求出恰好符合条件时两个图形各运动了多少时间；若不存在，请说明理由．
△ABC的边长AB=1厘米，AC=
2
厘米，BC=
3
厘米，则其外接圆的半径是
3
2
厘米
3
2
厘米
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网