题目内容
△ABC的边长AB=1厘米,AC=
厘米,BC=
厘米,则其外接圆的半径是
厘米
厘米.
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
分析:根据勾股定理的逆定理求出∠CAB=90°,根据直角三角形外接圆的半径等于斜边的一半求出即可.
解答:解:
∵AB2+AC2=12+(
)2=3,BC2=(
)2=3,
∴AB2+AC2=BC2,
∴∠CAB=90°,
∴△ABC的外接圆的半径等于AD(或BD或CD)的长,是
BC=
厘米,
故答案为:
厘米.

∵AB2+AC2=12+(
| 2 |
| 3 |
∴AB2+AC2=BC2,
∴∠CAB=90°,
∴△ABC的外接圆的半径等于AD(或BD或CD)的长,是
| 1 |
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了勾股定理的逆定理,直角三角形的性质,三角形的外接圆等知识点,注意:直角三角形的外接圆的半径等于斜边的一半.

练习册系列答案
相关题目
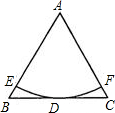 如图,正△ABC的边长AB=2,以A为圆心的圆切BC于点D,交AB于点E,交AC于点F,则弧EF的长=
如图,正△ABC的边长AB=2,以A为圆心的圆切BC于点D,交AB于点E,交AC于点F,则弧EF的长= △ABC的边长AB=2,面积为1,直线PQ∥BC,分别交AB、AC于P、Q,设AP=t,△APQ面积为S,则S关于t的函数图象大致是( )
△ABC的边长AB=2,面积为1,直线PQ∥BC,分别交AB、AC于P、Q,设AP=t,△APQ面积为S,则S关于t的函数图象大致是( )