题目内容
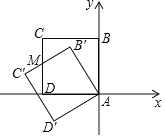
【题目】如图，正方形ABCD的边长为1，点A与原点重合，点B在y轴的正半轴上，点D在x轴的负半轴上，将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置，B′C′与CD相交于点M，则M的坐标为（ ）
A.（1，
）B.（﹣1，）C.（1，
）D.（﹣1，）
【答案】B
【解析】
连接AM，易得∠B′AD＝60°，利用HL判定Rt△ADM≌Rt△AB′M，进而得到∠DAM＝30°，再根据DM＝AD·tan∠DAM求出DM，即可得到M的坐标.
解：如图，连接AM，
∵将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C′D′，
∴AD＝AB′＝1，∠BAB′＝30°，
∴∠B′AD＝60°，
在Rt△ADM和Rt△AB′M中，
∴Rt△ADM≌Rt△AB′M（HL），
∴∠DAM＝∠B′AM＝
∠B′AD＝30°，
∴DM＝AD·tan∠DAM＝1×
＝，
∴点M的坐标为（﹣1，），
故选：B．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
相关题目
