题目内容
设方程x2+px+q=0的两根x1，x2均为正整数，若p+q=28，则（x1-1）（x2-1）=分析：首先利用根与系数的关系得出有关x1，x2的方程，利用质数的性质得出方程的解．
解答：解．x1+x2=-p，x1x2=q，p+q=x1x2-x1-x2=28，X1=
=1+
，因为两根均为正整数，且29为质数，所以x2=2 或 x2=30，即方程可化为（x-2）（x-30）=0，∴方程的两根分别为2，30，
（x1-1）（x2-1）=29．
故填：29．
| 28+x2 |
| x2-1 |
| 29 |
| x2-1 |
（x1-1）（x2-1）=29．
故填：29．
点评：此题主要考查了一元二次方程根与系数的关系以及质数的性质，题目比较典型．
练习册系列答案
相关题目
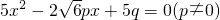有两个相等的实数根．
．
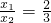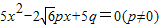有两个相等的实数根．
．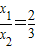