题目内容
已知关于x的一元二次方程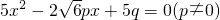 有两个相等的实数根.
有两个相等的实数根.
求证:(1)方程x2+px+q=0有两个不相等的实数根;
(2)设方程x2+px+q=0的两个实数根是x1,x2,若|x1|<|x2|,则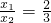 .
.
证明:(1)∵一元二次方程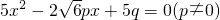 有两个相等的实数根,
有两个相等的实数根,
∴(-2 p)2-4×5×5q=0,
p)2-4×5×5q=0,
整理得6p2-25q=0,即p2= q,且q>0,
q,且q>0,
∴对于方程x2+px+q=0,△=p2-4q= q-4q=
q-4q= q,
q,
∵q>0,
∴△>0,
∴方程x2+px+q=0有两个不相等的实数根;
(2)∵6p2-25q=0,
∴q= ,
,
∴x2+px+ =0,即25x2+25px+6p2=0,
=0,即25x2+25px+6p2=0,
∴(5x+3p)(5x+2p)=0,
∵|x1|<|x2|,
∴x1=- ,x2=-
,x2=- ,
,
∴ =
= .
.
分析:(1)由于一元二次方程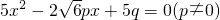 有两个相等的实数根,根据判别式的意义得到(-2
有两个相等的实数根,根据判别式的意义得到(-2 p)2-4×5×5q=0,则6p2-25q=0,即p2=
p)2-4×5×5q=0,则6p2-25q=0,即p2= q,且q>0,再计算方程x2+px+q=0的△=p2-4q=
q,且q>0,再计算方程x2+px+q=0的△=p2-4q= q-4q=
q-4q= q,由q>0得到△>0,可判断方程x2+px+q=0有两个不相等的实数根;
q,由q>0得到△>0,可判断方程x2+px+q=0有两个不相等的实数根;
(2)由6p2-25q=0得q= ,代入方程x2+px+q=0整理得到25x2+25px+6p2=0,即(5x+3p)(5x+2p)=0,由于|x1|<|x2|,则x1=-
,代入方程x2+px+q=0整理得到25x2+25px+6p2=0,即(5x+3p)(5x+2p)=0,由于|x1|<|x2|,则x1=- ,x2=-
,x2=- ,即可得到两根的比值.
,即可得到两根的比值.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=- ,x1•x2=
,x1•x2= .也考查了一元二次方程根的判别式.
.也考查了一元二次方程根的判别式.
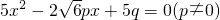 有两个相等的实数根,
有两个相等的实数根,∴(-2
 p)2-4×5×5q=0,
p)2-4×5×5q=0,整理得6p2-25q=0,即p2=
 q,且q>0,
q,且q>0,∴对于方程x2+px+q=0,△=p2-4q=
 q-4q=
q-4q= q,
q,∵q>0,
∴△>0,
∴方程x2+px+q=0有两个不相等的实数根;
(2)∵6p2-25q=0,
∴q=
 ,
,∴x2+px+
 =0,即25x2+25px+6p2=0,
=0,即25x2+25px+6p2=0,∴(5x+3p)(5x+2p)=0,
∵|x1|<|x2|,
∴x1=-
 ,x2=-
,x2=- ,
,∴
 =
= .
.分析:(1)由于一元二次方程
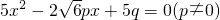 有两个相等的实数根,根据判别式的意义得到(-2
有两个相等的实数根,根据判别式的意义得到(-2 p)2-4×5×5q=0,则6p2-25q=0,即p2=
p)2-4×5×5q=0,则6p2-25q=0,即p2= q,且q>0,再计算方程x2+px+q=0的△=p2-4q=
q,且q>0,再计算方程x2+px+q=0的△=p2-4q= q-4q=
q-4q= q,由q>0得到△>0,可判断方程x2+px+q=0有两个不相等的实数根;
q,由q>0得到△>0,可判断方程x2+px+q=0有两个不相等的实数根;(2)由6p2-25q=0得q=
 ,代入方程x2+px+q=0整理得到25x2+25px+6p2=0,即(5x+3p)(5x+2p)=0,由于|x1|<|x2|,则x1=-
,代入方程x2+px+q=0整理得到25x2+25px+6p2=0,即(5x+3p)(5x+2p)=0,由于|x1|<|x2|,则x1=- ,x2=-
,x2=- ,即可得到两根的比值.
,即可得到两根的比值.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .也考查了一元二次方程根的判别式.
.也考查了一元二次方程根的判别式. 
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.