题目内容
8.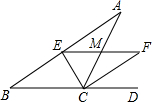 如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=3.5,则CE2+CF2的值为49.
如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=3.5,则CE2+CF2的值为49.
分析 根据角平分线的定义推出△ECF为直角三角形,然后根据勾股定理求得CE2+CF2=EF2,即可得出结果.
解答 解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=$\frac{1}{2}$∠ACB,∠ACF=$\frac{1}{2}$∠ACD,
即∠ECF=$\frac{1}{2}$(∠ACB+∠ACD)=90°,
又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,
∴CM=EM=MF=5,
∴EF=7,
由勾股定理得:CE2+CF2=EF2=49.
点评 本题考查角平分线的定义、勾股定理、直角三角形的判定;熟练掌握勾股定理,证明三角形是直角三角形是解决问题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.下列说法中,正确的个数有( )
(1)绝对值最小的数是1和-1.
(2)多项式-3a2b+7a2b2-2ab+1的项数是4.
(3)数轴上与表示-2的点距离3个长度单位的点所表示的数是1.
(4)若|x|=-x,则x<0.
(1)绝对值最小的数是1和-1.
(2)多项式-3a2b+7a2b2-2ab+1的项数是4.
(3)数轴上与表示-2的点距离3个长度单位的点所表示的数是1.
(4)若|x|=-x,则x<0.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20.下列各组代数式中,不是同类项的一组是( )
| A. | 5x2y和-yx2 | B. | -32和3 | C. | 3xy和-$\frac{xy}{2}$ | D. | x2y和2xy2 |