题目内容
16. 如图,在△ABC中,∠C=90°,AC=3,BC=4,AB=5,角平分线AF和BG交于D,DE⊥AB于E,则DE长为1.
如图,在△ABC中,∠C=90°,AC=3,BC=4,AB=5,角平分线AF和BG交于D,DE⊥AB于E,则DE长为1.
分析 过D作DM⊥AC于M,DN⊥BC于N,连接CD,根据AF和BG分别平分∠BAC,∠ABC,得到四边形DNCM是正方形,设DN=CN=CM=DM=r,根据三角形的面积列方程即可求得结果.
解答  解:过D作DM⊥AC于M,DN⊥BC于N,连接CD,
解:过D作DM⊥AC于M,DN⊥BC于N,连接CD,
∵AF和BG分别平分∠BAC,∠ABC,
∴DE=DM=DN,
∴四边形DNCM是正方形,
∴DN=CN=CM=DM,
设DN=CN=CM=DM=r,
∴S△ABC=S△ADB+S△BCD+S△ADC,
∴$\frac{1}{2}$(AB+AC+BC)r=$\frac{1}{2}×3×4$,
∴r=1,
∴DE=1.
故答案为:1.
点评 本题考查了角平分线的性质,三角形的内心的性质三角形面积,熟练掌握各性质定理是解题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
4.若式子$\frac{\sqrt{5x+10}}{x-3}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥-2 且x≠3 | B. | x≥-2 | C. | x≤-2且x≠0 | D. | x>-2且x≠3 |
11.下列说法中正确的是( )
| A. | 数据-2,1,3,4,4,5的中位数是4 | |
| B. | 想了解某种饮料中含色素的情况,宜采用抽样调查 | |
| C. | 数据1,1,2,2,3的众数是3 | |
| D. | 一组数据的波动越大,方差越小 |
1.下列说法中不正确的是( )
| A. | 绝对值最小的数是0 | |
| B. | 任何负数的绝对值都是它的相反数 | |
| C. | 任何有理数的绝对值都不可能是负数 | |
| D. | 互为相反数的两个数,一定一个是正数,一个是负数 |
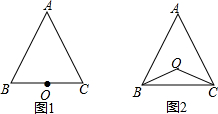 已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.