题目内容
如图，以等腰直角三角形ABC的斜边AB为边作等边△ABD，连接DC，以DC为边作等边△DCE，点B、E在C、D的同侧，若AB=
，求BE的长.
解：因为△ABD和△CDE是等边三角形，
所以AD=BD，CD=DE，∠ADB=∠CDE=60°.
所以∠ADB－∠CDB=∠CDE－∠CDB，即∠ADC=∠BDE.
在△ADC和△BDE中，因为AD=BD，CD=DE，∠ADC=∠BDE，
所以△ADC≌△BDE，所以AC=BE.
在等腰直角△ABC中，AB=，所以AC=BC=1，故BE=1.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
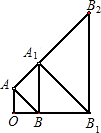如图，以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1，再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1，…，如此作下去，若OA=OB=1，则第2008个等腰直角三角形的面积S2008=
如图，以等腰直角三角形ABC的斜边AB与边面内作等边△ABD，连接DC，以DC当边作等边△DCE，B、E在C、D的同侧，若AB=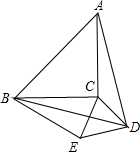
如图，以等腰直角三角形ABC的斜边AB为边向内作等边△ABD，连接DC，以DC为边作等边△DCE．B、E在C、D的同侧，若AB=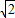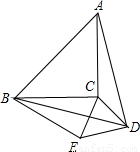
，则BE= ．
，则BE= ．