题目内容
若一次函数y=x+b的图象与两坐标围成的三角形面积为2，则b= ．
考点：一次函数图象上点的坐标特征
专题：探究型
分析：先令x=0求出y的值，再令y=0求出x的值，根据三角形的面积公式即可得出关于b的方程，求出b的值即可．
解答：解：∵令x=0，则y=b；令y=0，则x=-b，
∴一次函数y=x+b的图象与x、y轴的交点分别为（-b，0），（0，b），
∴
b2=2，
解得b=±2．
故答案为：±2．
∴一次函数y=x+b的图象与x、y轴的交点分别为（-b，0），（0，b），
∴
| 1 |
| 2 |
解得b=±2．
故答案为：±2．
点评：本题考查的是一次函数图象上点的坐标特点，熟知坐标轴上点的坐标特点是解答此题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
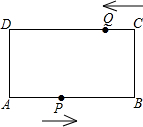如图，在矩形ABCD中，AB=24厘米，BC=10厘米，点P从A开始沿AB边以4厘米/秒的速度运动，点Q从C开始沿CD边2厘米/秒的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达终点时，另一点也随之停止运动，设运动时间为t秒．下列计算正确的是（ ）
| A、a3-a2=a |
| B、a•a2=a2 |
| C、（a2）3=a6 |
| D、a10÷a2=a5 |
已知：如图，一次函数y=kx+b的图象与x轴交于（-2，0），当y＞0时，x的取值范围是（ ）| A、x＜-2 | B、x＞-2 |
| C、x＞0 | D、x＜0 |
已知△ABC中，AB=AC，D是△ABC外接圆劣弧AC上的点（不与点A重合），延长BD到E．