题目内容
设 是反比例函数,则k=________;其图象经过第________象限;当x>0时,y随x的增大而________.
是反比例函数,则k=________;其图象经过第________象限;当x>0时,y随x的增大而________.
0 一、三 减小
分析:让x的次数为-1列式可得k的值,进而可得x的比例系数,根据比例系数的符号可得图象所在象限,以及每个象限内函数在增减性.
解答:∵ 是反比例函数,
是反比例函数,
∴2k2-1=-1,
解得k=0,
∴反比例的函数的比例系数为:k+2=2,
∴其图象经过第一、三象限;当x>0时,y随x的增大而减小.
故答案为:0;一、三;减小.
点评:考查反比例函数的定义及性质;用到的知识点为:反比例的一般形式也可以写成y=kx-1(k≠1);反比例函数的比例系数大于0,图象在一三象限,在每个象限内,y随x的增大而减小.
分析:让x的次数为-1列式可得k的值,进而可得x的比例系数,根据比例系数的符号可得图象所在象限,以及每个象限内函数在增减性.
解答:∵
 是反比例函数,
是反比例函数,∴2k2-1=-1,
解得k=0,
∴反比例的函数的比例系数为:k+2=2,
∴其图象经过第一、三象限;当x>0时,y随x的增大而减小.
故答案为:0;一、三;减小.
点评:考查反比例函数的定义及性质;用到的知识点为:反比例的一般形式也可以写成y=kx-1(k≠1);反比例函数的比例系数大于0,图象在一三象限,在每个象限内,y随x的增大而减小.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
设A( x1,y1)、B (x2,y2)是反比例函数y=-
图象上的两点.若x1<x2<0,则y1与y2之间的关系是( )
| 2 |
| x |
| A、y1<y2<0 |
| B、y2<y1<0 |
| C、y2>y1>0 |
| D、y1>y2>0 |
设A,B是反比例函数y=-
的图象上关于原点对称的两点,AD平行于y轴交x轴于D,BC平行于x轴交y轴于C,设四边形ABCD的面积S,则( )
| 3 |
| 2x |
A、s=
| ||
B、s=
| ||
C、s=
| ||
| D、s=6 |
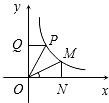 设P(a,b),M(c,d)是反比例函数y=
设P(a,b),M(c,d)是反比例函数y=