题目内容
若实数a、b满足a2+ab+b2=1,且t=ab-a2-b2,则t的取值范围是 ________.
-3≤t≤-
分析:首先将两式进行相加再相减,得出a+b,ab有关t的关系式,再构造一元二次方程,利用根的判别式大于等于0解决.
解答:∵ ,
,
∴解得:ab=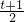 ,
,
∵a2+b2= ,
,
∴(a+b)2=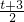 ≥0,
≥0,
∴-3≤t,
假设a,b是关于x的一元二次方程,
∴x 2+(a+b)x+ab=0,
∴x 2+ x+
x+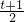 =0,
=0,
∵b2-4ac≥0,
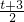 -2(t+1)≥0,
-2(t+1)≥0,
解得:t≤ .
.
则t的取值范围是:-3≤t≤ .
.
故答案为:-3≤t≤ .
.
点评:此题主要考查了根与系数的关系,利用两根构造一元二次方程,根据根的判别式求解,是解决问题的关键.

分析:首先将两式进行相加再相减,得出a+b,ab有关t的关系式,再构造一元二次方程,利用根的判别式大于等于0解决.
解答:∵
 ,
,∴解得:ab=
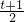 ,
,∵a2+b2=
 ,
,∴(a+b)2=
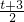 ≥0,
≥0,∴-3≤t,
假设a,b是关于x的一元二次方程,
∴x 2+(a+b)x+ab=0,
∴x 2+
 x+
x+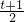 =0,
=0,∵b2-4ac≥0,
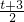 -2(t+1)≥0,
-2(t+1)≥0,解得:t≤
 .
.则t的取值范围是:-3≤t≤
 .
.故答案为:-3≤t≤
 .
.点评:此题主要考查了根与系数的关系,利用两根构造一元二次方程,根据根的判别式求解,是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若实数a、b满足a2-8a+5=0,b2-8b+5=0,则
+
的值是( )
| b-1 |
| a-1 |
| a-1 |
| b-1 |
| A、-20 | ||
| B、2 | ||
| C、2或-20 | ||
D、
|