Question

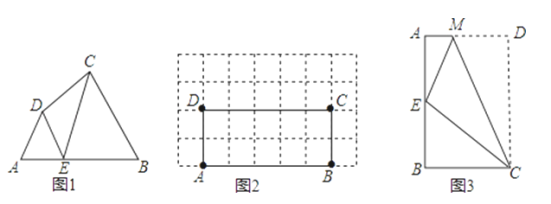
【题目】如图，已知矩形纸片BDEF和直角三角板BCA，点A在EF上，AC＝DE＝，FE＝3，∠C＝90°，∠CBA＝30°.

(1)写出三种不同类型的结论．

(2)将直角三角板绕点B旋转，在旋转过程中，

①求点A与点E的最短距离；

②若将直角三角板绕点B从①中位置开始顺时针旋转α度(0≤α≤360)，使∠BAE＝90°，求α的度数．

Answer 1

【答案】（1）见解析;(2)②2;②60°和300°.

【解析】

（1）在Rt△ABC中，由∠C=90°，AC=可以求出∠BAC，AB、BC，通过AB=2BF得∠FAB=30°，进而得到AG=BG；

（2）①如图，当A、B、E共线时，AE最小，求出BE长即可得；

②分两种情况画出图形，求出∠EBA′和∠EBA″即可.

（1）在Rt△ABC中，∵∠C=90°，AC＝，∠CBA＝30°，

∴AB=2AC=2，BC==3，

∠BAC=90°-∠ABC=60°，

∵四边形BDEF是矩形，

∴BF=ED=AC=，∠F=90°，

∴AB=2BF，∠FAB=30°，

∴∠GBA=∠GAB，

∴GB=GA，

三个不同类型的结论为：AB=2，∠BAC=90°=60°，GB=GA（答案不唯一，只要合理即可）；

(2)①如图，当点B，A，E三点共线时，AE最短，连接BE，

∵四边形BDEF是矩形，

∴∠D=90°，BD=EF=3，BF=DE=，

∴BE===4，

∴AE=BE-AB=4－2=2；

②在图1中，∵∠BA′E=90°，

∴cos∠EBA′=,

∴∠EBA′=60°，

同理，在图2中，∠A″BE=60°，

∴旋转角α=60°或300°.