题目内容
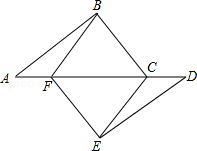
【题目】(问题背景)
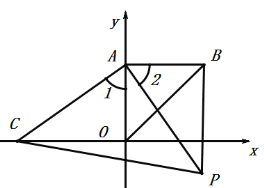
如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是
是![]() 轴上的一个动点.当点
轴上的一个动点.当点![]() 在
在![]() 轴上移动时,始终保持
轴上移动时,始终保持![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() (点
(点![]() 、
、![]() 、
、![]() 按逆时针方向排列);当点
按逆时针方向排列);当点![]() 移动到点
移动到点![]() 时,得到等腰直角三角形
时,得到等腰直角三角形![]() (此时点
(此时点![]() 与点
与点![]() 重合).
重合).
(初步探究)
(1)写出点![]() 的坐标______.
的坐标______.
(2)点![]() 在
在![]() 轴上移动过程中,当等腰直角三角形
轴上移动过程中,当等腰直角三角形![]() 的顶点
的顶点![]() 在第四象限时,连接
在第四象限时,连接![]() .
.
求证:![]() ;
;
(深入探究)
(3)当点![]() 在
在![]() 轴上移动时,点
轴上移动时,点![]() 也随之运动.经过探究发现,点
也随之运动.经过探究发现,点![]() 的横坐标总保持不变,请直接写出点
的横坐标总保持不变,请直接写出点![]() 的横坐标:______.
的横坐标:______.
(拓展延伸)
(4)点![]() 在
在![]() 轴上移动过程中,当
轴上移动过程中,当![]() 为等腰三角形时,直接写出此时点
为等腰三角形时,直接写出此时点![]() 的坐标.
的坐标.
 备用图
备用图
【答案】(1)(1,1);(2)证明见解析;(3)1;(4)![]() .
.
【解析】
根据等腰直角三角形的性质,OA=AB,题干中已知A点坐标,即可求得OB的长度,表示出B点坐标即可.
根据等腰直角三角形的性质得到![]() ,再根据等角的余角相等,得出角
,再根据等角的余角相等,得出角![]() ,最后利用三角形全等的判定方法进行判定即可.
,最后利用三角形全等的判定方法进行判定即可.
根据(2)的结论△ABP也为直角三角形,且AB垂直BP,且AB=OB=1,即可得出P点的横坐标.
先根据题意,确定B点、A点坐标,设出P点和C点坐标,分情况进行讨论,当OP=OB时,当OB=BP时,当OP=BP时,分别利用两点间距离公式求出点P点的坐标,然后分别算出AP的长,最后利用AP=AC计算出A点坐标即可.
解:(1)∵点A的坐标为(0,1)
△OAB是等腰直角三角形,且OA=AB,OA⊥BA
∴B点坐标为![]() .
.
(2)证明:在等腰直角三角形![]() 中,
中,![]() ,
,![]()
在等腰直角三角形![]() 中,
中,![]() ,
,![]()
![]()
![]()
![]()
在![]() 和
和![]() 中
中
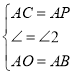
![]()
(3)![]() (已证)
(已证)
∴∠ABP=90°
∴PB垂直AB,P点在过B点且垂直与AB的垂线上,
∵点B的坐标为(1,1)
∴P点的横坐标为1.
(4)由题意和(1)可知![]() ,
,
设P(1,y),C(x,0),
当OB=OP时,![]() ,
,
解得:![]() 或
或![]() ,
,
则![]() 或
或![]() ,
,
解得:![]() ,
,
所以C点坐标为(![]() )或(
)或(![]() )
)
同理当OB=OP时,可得C点坐标为(-2,0)
当BP=OP时,可得C点坐标为(-1,0)
故答案为:![]()