题目内容
为响应“低碳生活”的号召,李明决定每天骑自行车上学,有一天李明骑了1000米后,自行车发生了故障,修车耽误了5分钟,车修好后李明继续骑行,用了8分钟骑行了剩余的800米,到达学校(假设在骑车过程中匀速行驶).若设他从家开始去学校的时间为t(分钟),离家的路程为y(千米),则y与t(15<t≤23)的函数关系为
- A.y=100t(15<t≤23)
- B.y=100t-500(15<t≤23)
- C.y=50t+650(15<t≤23)
- D.y=100t+500(15<t≤23)
B
分析:先求出骑车的速度,然后根据路程=故障前行走的路程+故障后行走的路程,即可得出y与x的函数关系式.
解答:∵用了8分钟骑行了剩余的800米,
∴速度v=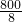 =100米/分,
=100米/分,
则可得y=1000+100(t-15)=100t-500(15<t≤23).
故选B.
点评:本题考查了根据实际问题抽象一次函数关系式的知识,属于基础题,解答本题的关键是求出速度.
分析:先求出骑车的速度,然后根据路程=故障前行走的路程+故障后行走的路程,即可得出y与x的函数关系式.
解答:∵用了8分钟骑行了剩余的800米,
∴速度v=
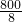 =100米/分,
=100米/分,则可得y=1000+100(t-15)=100t-500(15<t≤23).
故选B.
点评:本题考查了根据实际问题抽象一次函数关系式的知识,属于基础题,解答本题的关键是求出速度.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
