题目内容
4.某商场计划购进冰箱、彩电进行销售,已知冰箱的进货单价比彩电的进货单价多400元,若商场用80000元购进冰箱的数量与用64000元购进彩电的数量相等,该商场冰箱、彩电的售货单价如表:| 冰箱 | 彩电 | |
| 售价(元/台) | 2500 | 2000 |
(2)为了满足市场需求,商场决定用不超过90000元的资金采购冰箱、彩电共50台,若该商场将购进的冰箱、彩电共50台全部售出,获得利润为w元,为了使商场的利润最大,该商场如何购进冰箱、彩电,最大利润是多少?
分析 (1)设出冰箱、彩电的进货单价,列出方程组解答即可;
(2)设购买彩电x台,则购进冰箱(50-x)台,用含x的代数式表示利润W,根据x的取值范围和一次函数的性质求解.
解答 解:(1)设出冰箱、彩电的进货单价分别为x元,y元,可得:
$\left\{\begin{array}{l}{x=y+400}\\{\frac{80000}{x}=\frac{64000}{y}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2000}\\{y=1600}\end{array}\right.$,
答:冰箱、彩电的进货单价分别为2000元,1600元;
(2)设购买彩电x台,则购进冰箱(50-x)台,可得:
1600x+(1600+400)(50-x)≤90000
解得:x≥25,
由题意,得
W=(2000-1600)x+(2500-2000)(50-x),
=-100x+25000.
∵k=-100<0,
∴W随x的增大而减小,
∴x=25时,W最大=25000,
∴w的最大值为25000元.
点评 本题考查了列分式方程解实际问题的运用,一次函数的解析式的性质的运用,解答时根据总利润═冰箱的利润+洗衣机的利润建立解析式是关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
19.某县正在开展“拆临拆违”工作,某街道产生了m立方米的“拆临拆违”垃圾需要清理,一个工程队承包了清理工作,计划每天清理80立方米,考虑到还有其它地方的垃圾需要清理,该工程队决定增加人手以提高50%的清理效率,则完成整个任务的实际时间比原计划时间少用了( )
| A. | $\frac{m}{240}$天 | B. | $\frac{m}{250}$天 | C. | $\frac{m}{260}$天 | D. | $\frac{m}{270}$天 |
9.下列各式能用完全平方公式分解的是( )
| A. | y2-18y+9 | B. | 4x2+6x+9 | C. | x2-8x-16 | D. | -a2+4ab-4b2 |
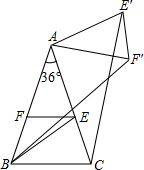 如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.
如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB. 如图,AB∥CD,∠1=120°,∠ECD=70°,∠E的大小是50°.
如图,AB∥CD,∠1=120°,∠ECD=70°,∠E的大小是50°. 如图,方格纸中有一条可爱美丽的小金鱼
如图,方格纸中有一条可爱美丽的小金鱼