题目内容
9、有两组数据如表，下列结论中正确的是（ ）
|
分析：分别代入方差公式求得甲乙两人的方差，比较即可．
解答：解：通过观察两组数据发现：甲组数据均减去20可以得到新数据：0、1、3、4、6，
乙组数据均减去100可以得到新数据：0、1、3、4、6
∵一组数据均减去一个常数后，新数据的方差等于原数据的方差，
∴两组数据的方差相等．
故选C．
乙组数据均减去100可以得到新数据：0、1、3、4、6
∵一组数据均减去一个常数后，新数据的方差等于原数据的方差，
∴两组数据的方差相等．
故选C．
点评：本题考查了方差的计算，除了可以用上述方法外还可以通过分别计算两组数据的方差后进行比较．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
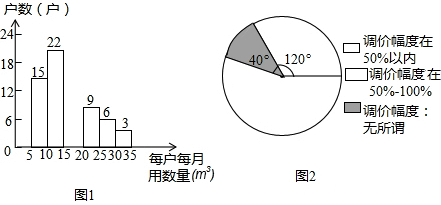
水是生命之源．长期以来，某市由于水价格不合理，一定程度上造成了水资源的浪费．为改善这一状况，相关部门正在研究制定居民用水价格调整方案．小明想为政府决策提供信息，于是在某小区内随机访问了部分居民，就每月的用水量、可承受的水价调整的幅度等进行调查，并把调查结果整理成如图．
已知被调查居民每户每月的用水量在5m3-35m3之间，被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户，试回答下列问题：
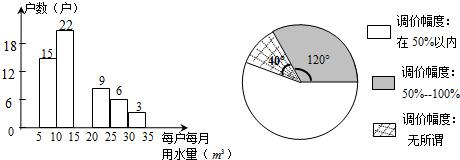
（1）如图使用的统计图表的名称是 ，它是表示一组数据 的量；
（填“平均水平”、“离散程度”或“分布情况”）
（2）上述两个统计图表是否完整，若不完整，试把它们补全；
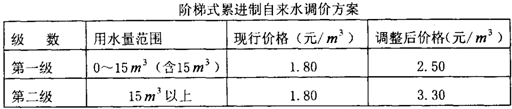
（3）若采用阶梯式累进制调价方案（如表1所示），试估计该小区有百分之几的居民用水费用的增长幅度不超过50%？
表一：阶梯式累进制调价方案
已知被调查居民每户每月的用水量在5m3-35m3之间，被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户，试回答下列问题：
（1）如图使用的统计图表的名称是
（填“平均水平”、“离散程度”或“分布情况”）
（2）上述两个统计图表是否完整，若不完整，试把它们补全；
（3）若采用阶梯式累进制调价方案（如表1所示），试估计该小区有百分之几的居民用水费用的增长幅度不超过50%？
表一：阶梯式累进制调价方案
| 级数 | 用水量范围 | 现行价格 | 调整后的价格 |
| 第一级 | 0-15m3（含15m3） | 1.80 | 2.50 |
| 第二级 | 15m3以上 | 1.80 | 3.30 |
关数据回答下列问题：
