题目内容
如图,等边△OAB的边OB在x轴的负半轴上,双曲线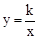 过OA的中点,已知等边三角形的边长是4,则该双曲线的表达式为
过OA的中点,已知等边三角形的边长是4,则该双曲线的表达式为
A.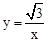 | B. | C. | D. |
B
解析试题分析:如图,过点C作CD⊥OB于点D.
∵△OAB是等边三角形,该等边三角形的边长是4,
∴OA=4,∠COD=60°。
又∵点C是边OA的中点,∴OC=2。
∴OD=OC•cos60°=2× =1,CD=OC•sin60°=2×
=1,CD=OC•sin60°=2× =
= 。
。
∴C(﹣1, )。
)。
∵双曲线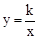 过OA的中点C,∴
过OA的中点C,∴ ,解得,k=﹣
,解得,k=﹣ 。
。
∴该双曲线的表达式为 .
.
故选B。

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
双曲线 与直线y=2x+1的一个交点横坐标为﹣1,则k=( )
与直线y=2x+1的一个交点横坐标为﹣1,则k=( )
| A.﹣2 | B.﹣1 | C. 1 | D.2 |
已知矩形的面积为8,则它的长y与宽x之间的函数关系用图象大致可以表示为
A. | B. | C. | D. |
当 时,函数
时,函数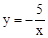 的图象在【 】
的图象在【 】
| A.第四象限 | B.第三象限 | C.第二象限 | D.第一象限 |
如图,点P(﹣3,2)是反比例函数 (k≠0)的图象上一点,则反比例函数的解析式【 】
(k≠0)的图象上一点,则反比例函数的解析式【 】
A. | B. | C. | D. |
 (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y=
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y= (x>0); ④
(x>0); ④ ,其中正确的结论有( )个。
,其中正确的结论有( )个。
 (k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是
(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是
 图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有
图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有
 (x>0)的图象上,则OB2—OA2的值为 .
(x>0)的图象上,则OB2—OA2的值为 .