题目内容
在△ABC和△DEF中，∠A=∠D，AB=4，BC=5，AC=6，EF=10，如果△ABC与△DEF相似，那么DE= ．
【答案】分析：已知△ABC与△DEF相似，且∠A、∠D是对应角，但没有明确另外两组对应角分别是哪些角，因此要分情况讨论．
解答：解：△ABC和△DEF中，∠A=∠D，若△ABC∽△DEF，可分两种情况：
①∠B=∠E，则AB：DE=BC：EF，即DE=
=8；
②∠B=∠F，则AC：DE=BC：EF，即DE=
=12．
故DE的长为8或12．
点评：此题主要考查了相似三角形的性质；在不确定相似三角形的对应角和对应边的情况下，要将各种情况都考虑到，以免漏解．
解答：解：△ABC和△DEF中，∠A=∠D，若△ABC∽△DEF，可分两种情况：
①∠B=∠E，则AB：DE=BC：EF，即DE=
=8；②∠B=∠F，则AC：DE=BC：EF，即DE=
=12．故DE的长为8或12．
点评：此题主要考查了相似三角形的性质；在不确定相似三角形的对应角和对应边的情况下，要将各种情况都考虑到，以免漏解．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
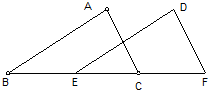20、如图，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件，请你在其中选3个作为条件，余下的1个作为结论，使其成为一个真命题，并加以证明．
如图所示，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有六个条件，请你在其中选三个作为已知条件，余下的选一个作为结论，编写出一个真命题，并说明理由．①AB=DE；②AC=DF；③∠ABC=∠DEF；④BE=CF；⑤∠ACB=∠DEF；⑥∠A=∠D（填写序号即可）
如图，已知BC∥EF，且BC=EF，AF=CD，则AB=DE，说明理由．