题目内容
.观察图,解答后面的问题.
梯形个数1 2 3 4 5 6…周长5 8 11 14…

(1)把表中的空格填上适当的数据:
梯形个数 1 2 3 4 5 6 …
周长 5 8 11 14 …
(2)写出周长L和梯形个数n之间的二元一次方程;
(3)求n=2015时L的值;
(4)求L=6053时n的值.
解:(1)由图中可以看出图形的周长=上下底的和+两腰长,
梯形个数为1时,周长为3+2=5;
梯形个数为2时,周长为2×3+2=8;
梯形个数为3时,周长为3×3+2=11;
…
L=3n+2.
当n=5时,L=3×5+2=17.
当n=6时,L=3×6+2=20.
故答案是:17;20.
(2)由(1)知,周长L和梯形个数n之间的二元一次方程是:L=3n+2.
(3)当n=2015时,L=3×2015+2=6047;
(4)当L=6053时,3n+2=6043,解得n=2017.
点评: 本题考查二元一次方程的应用,图形的规律性变化,根据图形中不变的量和变化的量得到相应图形的周长的变化规律是解决本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 连接CE并延长交AD于F.
连接CE并延长交AD于F. 1) 求证:△AEF≌△BEC;
1) 求证:△AEF≌△BEC;
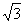 ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
 .其中2sin30°≤ a ≤ 3cos30°,且a为整数.
.其中2sin30°≤ a ≤ 3cos30°,且a为整数.