题目内容
19.若单项式$\frac{1}{2}$x2ya与-2xby3的和仍为单项式,则这两个单项式的和为-$\frac{3}{2}$x2y3.分析 根据题意可知单项式$\frac{1}{2}$x2ya与-2xby3是同类项,故此可求得a、b的值,然后再合并这两个单项式即可.
解答 解:∵单项式$\frac{1}{2}$x2ya与-2xby3的和仍为单项式,
∴单项式$\frac{1}{2}$x2ya与-2xby3是同类项.
∴a=3,b=2.
∴$\frac{1}{2}$x2ya+(-2xby3)=$\frac{1}{2}$x2y3-2x2y3=($\frac{1}{2}$-2)x2y3=-$\frac{3}{2}$x2y3.
故答案为:-$\frac{3}{2}$x2y3.
点评 本题主要考查的是同类项、合并同类项,掌握同类项的定义是解题的关键.

练习册系列答案
相关题目
9.下列图形绕某点旋转180°后,不能与原来图形重合的是( )
| A. |  | B. |  | C. |  | D. |  |
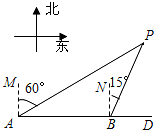 一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向上.
一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向上.