题目内容
(本题满分10分)大润发超市以每件30元的价格购进一种商品,试销中发现每天的销售量 (件)与每件的销售价
(件)与每件的销售价 (元)之间满足一次函数
(元)之间满足一次函数 .
.
(1)写出超市每天的销售利润 (元)与每件的销售价x(元)之间的函数关系式;
(元)与每件的销售价x(元)之间的函数关系式;
(2)如果超市每天想要获得销售利润420元,则每件商品的销售价应定为多少元?
(3)如果超市要想获得最大利润,每件商品的销售价定为多少元最合适?最大销售利润为多少元?
(1)w=-3 +252x-4860;(2)40或44;(3)42元,432元.
+252x-4860;(2)40或44;(3)42元,432元.
【解析】
试题分析:(1)根据销售利润=单件利润×数量求出;(2)根据w=420求出x的值;(3)将二次函数配方成顶点式,然后进行说明.
试题解析:(1)

∴
(2)由题意知:
∴

∴
 ∴当销售价定为40或44元时,可获得420元的利润.
∴当销售价定为40或44元时,可获得420元的利润.
(3) ∴
∴
∴当销售价定为42元时,所获得的利润最大.最大利润为432元.
考点:二次函数的应用.

练习册系列答案
相关题目
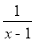 )÷
)÷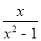 ,再选择一个恰当的x值代人并求值.
,再选择一个恰当的x值代人并求值.

 、0.2、
、0.2、 、
、 、
、 、
、 中,无理数的个数是( )
中,无理数的个数是( )
 ,并写出点
,并写出点 的坐标是 ;
的坐标是 ; ,使
,使 的坐标是 ;
的坐标是 ; ∥
∥ ∥
∥ ,
, ,
, ,那么
,那么 的值是 .
的值是 .
 的一元二次方程
的一元二次方程
 ,且两条直角边的长 b和c恰好是这个方程的两个根,求
,且两条直角边的长 b和c恰好是这个方程的两个根,求 的值
的值