题目内容
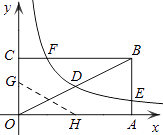
【题目】如图,反比例函数y= ![]() (x>0)的图象与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,若OC=2BD,则实数k的值为( )
(x>0)的图象与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,若OC=2BD,则实数k的值为( ) 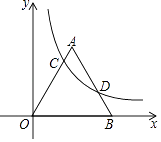
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F, 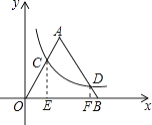
设OC=2x,则BD=x,
在Rt△OCE中,∠COE=60°,
则OE=x,CE= ![]() x,
x,
则点C坐标为(x, ![]() x),
x),
在Rt△BDF中,BD=x,∠DBF=60°,
则BF= ![]() x,DF=
x,DF= ![]() x,
x,
则点D的坐标为(5﹣ ![]() x,
x, ![]() x),
x),
将点C的坐标代入反比例函数解析式可得:k= ![]() x2 ,
x2 ,
将点D的坐标代入反比例函数解析式可得:k= ![]() x﹣
x﹣ ![]() x2 ,
x2 ,
则 ![]() x2=
x2= ![]() x﹣
x﹣ ![]() x2 ,
x2 ,
解得:x1=2,x2=0(舍去),
故k= ![]() x2=
x2= ![]() ×4=4
×4=4 ![]() .
.
故选A.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
相关题目