题目内容
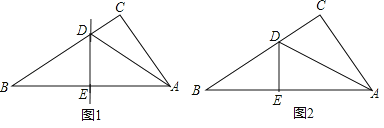
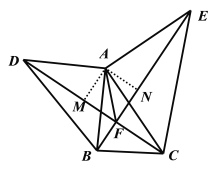
【题目】如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE。连结DC、BE交于F点。

(1)求证:△DAC≌△BAE;
(2)求证:DC⊥BE;
(3)求证:∠DFA=∠EFA.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)由题意可得AD=AB,AC=AE,由∠DAB=∠CAE=90°,可得到∠DAC=∠BAE,从而可证△DAC≌△BAE;
(2)由(1)可得∠ACD=∠AEB,再利用直角三角形的性质及等量代换即可得到结论;
(3)作AM⊥DC于M,AN⊥BE于N,利用全等三角形的面积相等及角平分线的判定即可证得结论.
证明:(1)∵![]()
![]() ,
,
∴![]() ,
,
即![]() ,
,
又∵![]() ,AC=AE,
,AC=AE,
∴△DAC≌△BAE;
(2)∵△DAC≌△BAE,
∴∠ACD=∠AEB,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∵![]() ≌
≌![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的平分线,
的平分线,
即![]() .
.
故答案为:(1)证明见解析;(2)证明见解析;(3)证明见解析.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目