题目内容
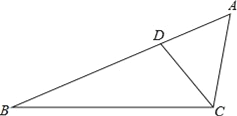
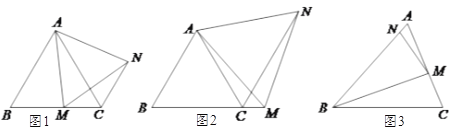
【题目】(Ⅰ)如图1,在等边![]() 中,点
中,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() ,
, ![]() ),连结
),连结![]() ,以
,以![]() 为边作等边
为边作等边![]() ,并连结
,并连结![]() .求证:
.求证: ![]() .
.
(Ⅱ)【类比探究】
如图2,在等边![]() 中,若点
中,若点![]() 是
是![]() 延长线上的任意一点(不含端点
延长线上的任意一点(不含端点![]() ),其它条件不变,则
),其它条件不变,则![]() 是否还成立?若成立,请说明理由;若不成立,请写出
是否还成立?若成立,请说明理由;若不成立,请写出![]() ,
, ![]() ,
, ![]() 三者间的数量关系,并给予证明.
三者间的数量关系,并给予证明.
(Ⅲ)【拓展延伸】
如图3,在等腰![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 上的任意一点(不含端点),连结
上的任意一点(不含端点),连结![]() ,以
,以![]() 为边作等腰
为边作等腰![]() ,使
,使![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(Ⅰ)证明见解析(Ⅱ)结论不成立(Ⅲ)![]()
【解析】试题分析:(Ⅰ)通过证明 ![]() ≌
≌![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() ,从而证得
,从而证得![]() ;
;
(Ⅱ)结论不成立,通过证明 ![]() ≌
≌![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() ,由
,由![]() ,得
,得![]() ;
;
(Ⅲ)![]() ,设
,设![]() ,由
,由![]() 为
为![]() 的外角,可得
的外角,可得![]() ,从而可得
,从而可得![]() ,又
,又![]() 为
为![]() 的外角,可得
的外角,可得![]() ,从而有
,从而有![]() ,继而推得
,继而推得![]() .
.
试题解析:(Ⅰ)∵![]() ,
, ![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() 即
即![]() ,
,
在![]() 和
和![]() 中,
中, 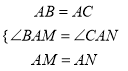 ,
,
![]()
![]() ≌
≌![]()
![]() ,
,
∴![]() ,
,
∴![]() ;
;
(Ⅱ)结论不成立,
理由: ![]() ,
, ![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() 即
即![]() ,
,
在![]() 和
和![]() 中,
中, 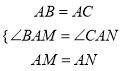 ,
,
![]()
![]() ≌
≌![]()
![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ;
;
(Ⅲ)![]() ,理由:
,理由:
设![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() 为
为![]() 的外角,
的外角,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,
又![]() 为
为![]() 的外角,
的外角,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目