题目内容
已知:如图,在正方形ABCD中,AD = 1,P、Q分别为AD、BC上两点,且AP=CQ,连结AQ、BP交于点E,EF平行BC交PQ于F,AP、BQ分别为方程![]() 的两根.(1)求
的两根.(1)求![]() 的值(2)试用AP、BQ表示EF
的值(2)试用AP、BQ表示EF
(3)若S△PQE =![]() ,求n的值
,求n的值
 |
(1)∵AP=QC,AP+BQ=QC+BQ=BC=1
又∵AP、BQ分别为方程![]() 的两根,有AP+BQ=m,AP?BQ=n
的两根,有AP+BQ=m,AP?BQ=n
∴AP+BQ=m=1(2分)
(2)∵EF∥AP∴![]() 又∵AP∥BQ∴
又∵AP∥BQ∴![]()
∴![]() 即
即![]()
∴![]() 即:
即:![]()
(3)连结QD,则EP∥QD,得:S△AQD=![]() ,且S△AEP∶S△AQD=AP2∶AD2= AP2∶1= AP2
,且S△AEP∶S△AQD=AP2∶AD2= AP2∶1= AP2
∴S△AEP= AP2?S△AQD= ![]() AP2 ∴S△PQE∶S△AEP=EQ∶AE,
AP2 ∴S△PQE∶S△AEP=EQ∶AE,
即![]() ∶
∶![]() AP2= EQ∶AE=BQ∶AP ∴AP?BQ=
AP2= EQ∶AE=BQ∶AP ∴AP?BQ=![]() 即:n=
即:n=![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
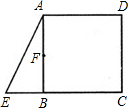 已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=
已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=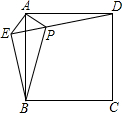 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=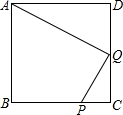 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?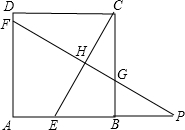 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.
已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.