Question

19．如图，矩形ABCD中，AD=5，AB=8，点E为DC上一个动点，把△ADE沿AE折叠，若点D的对应点D′，连接D′B，以下结论中：
①D′B的最小值为3；
②当DE=$\frac{5}{2}$时，△ABD′是等腰三角形；
③当DE=2是，△ABD′是直角三角形；
④△ABD′不可能是等腰直角三角形；
其中正确的有①②④．（填上你认为正确结论的序号）

Answer 1

分析 解：当D′落在线段AB上时，D′B的值最小，此时D′B=AB-AD=3，得出①正确；
过D′作MN⊥AB交AB于点N，交CD于点M，设AN=x，则EM=x-2.5，证出∠ED′M=∠D′AN，因此△EMD′∽△D′NA，得出对应边成比例$\frac{ED′}{AD′}$=$\frac{EM}{D′N}$，求出x=4，得出AN=BN，因此AD′=D′B，得出②正确；
当DE=2时，假设△ABD′是直角三角形，则E、D′、B在一条直线上，作EF⊥AB于点F，由勾股定理求出D′B、EB，得出③不正确；
当AD′=D′B时，由勾股定理的逆定理得出△ABD′不是直角三角形，当△ABD′是直角三角形时，由勾股定理求出D′B，得出AD′≠D′B，因此△ABD′不可能是等腰直角三角形，得出④正确．

解答 解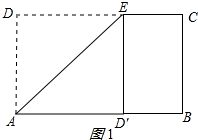：当D′落在线段AB上时，D′B的值最小，如图1所示：
此时D′B=AB-AD=8-5=3，
∴①正确；
过D′作MN⊥AB交AB于点N，交CD于点M，如图2所示：
设AN=x，则EM=x-2.5，
∵∠AD′N=∠DAD′，∠ED′M=180°-∠AD′E-∠AD′N=180°-90°-∠AD′N=90°-∠AD′N，
∴∠ED′M=90°-∠DAD′，
∵∠D′AN=90°-∠DAD′，
∴∠ED′M=∠D′AN，
∵MN⊥AB，
∴∠EMD′=∠AND′，
∴△EMD′∽△D′NA，
∴$\frac{ED′}{AD′}$=$\frac{EM}{D′N}$，
即$\frac{2.5}{5}$=$\frac{x-2.5}{\sqrt{{5}^{2}-{x}^{2}}}$，
解得：x=4，
∴AN=BN，
∴AD′=D′B，
即△ABD′是等腰三角形，
∴②正确；
当DE=2时，假设△ABD′是直角三角形，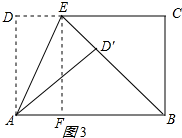
则E、D′、B在一条直线上，
作EF⊥AB于点F，如图3所示：
D′B=$\sqrt{A{B}^{2}-D′{A}^{2}}$=$\sqrt{{8}^{2}-{5}^{2}}$=$\sqrt{39}$，EB=$\sqrt{E{F}^{2}+F{B}^{2}}$=$\sqrt{{5}^{2}+（8-2）^{2}}$=$\sqrt{61}$，
∵2+$\sqrt{39}$≠$\sqrt{61}$，
∴③不正确；
当AD′=D′B时，5²+5²≠8²，
∴△ABD′不是直角三角形，
当△ABD′是直角三角形时，D′B=$\sqrt{A{B}^{2}-D′{A}^{2}}$=$\sqrt{{8}^{2}-{5}^{2}}$=$\sqrt{39}$，
∴AD′≠D′B，
∴△ABD′不可能是等腰直角三角形，
∴④正确；
故答案为：①②④．

点评 本题考查了矩形的性质、翻折变换的性质、勾股定理、等腰三角形的判定、勾股定理的逆定理、等腰直角三角形的判定等知识；本题综合性强，有一定难度，熟练掌握矩形的性质和翻折变换的性质是解决问题的关键．