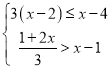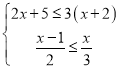题目内容
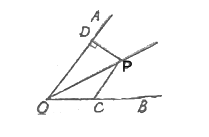
【题目】如图,点![]() 是
是![]() 的角平分线上一点,过点
的角平分线上一点,过点![]() 作
作 ![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() =__________.
=__________.
【答案】![]()
【解析】
过点P作PE⊥OB于点E.由角平分线的性质可知PD=PE,由OP是角平分线和PC∥OA,可得OC=PC=4,在直角三角形PCE中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半,故CE=2,再由勾股定理得PE的值即可得到PD的值.
解:如图,过点P作PE⊥OB于点E.

∵∠AOB=60°,点P是∠AOB的角平分线上一点,
∴∠POD=∠POC=30°,
又∵PC∥OA,
∴∠PCB=∠AOB=60°,∴∠POC=30°,
∵∠PCO=180°-∠60°=120°,
∴∠POC=∠OPC=30°,
∴△OCP为等腰三角形,
∵OC=4,∠PCE=60°,
∴PC=4,CE=2,PE=![]() =2
=2![]()
所以PD=PE=2![]()
故答案为2![]() .
.

练习册系列答案
相关题目