题目内容
10、当k为何实数时，方程x2+（k+1）x+2=0和方程x2-x-k=0有且只有一个相同的实数根，并求出这个相同的根．
分析：由方程x2+（k+1）x+2=0和方程x2-x-k=0相等的根联立解得这个相同的根和k的值．
解答：解：∵方程x2+（k+1）x+2=0和方程x2-x-k=0有且只有一个相同的实数根，
∴x+k+（k+1）x+2=0，
（k+2）x+k+2=0，
解得x=-1．
则方程的公共根是x=-1
代入方程x2+（k+1）x+2=0得到：1-k-1+2=0
解得k=-2．
∴x+k+（k+1）x+2=0，
（k+2）x+k+2=0，
解得x=-1．
则方程的公共根是x=-1
代入方程x2+（k+1）x+2=0得到：1-k-1+2=0
解得k=-2．
点评：本题主要考查一元二次方程根的判别式，是一个综合性的题目，也是一个难度中等的题目．
练习册系列答案
名校课堂系列答案
相关题目
，试求实数m的值．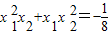
，试求实数m的值．