Question

15．如图，四边形OABC为矩形，点A，C分别在x轴和y轴上，连接AC，点B的坐标为（4，3），∠CAO的平分线与y轴相交于点D，则点D的坐标为（0，$\frac{4}{3}$）．

Answer 1

分析 过D作DE⊥AC于E，根据矩形的性质和B的坐标求出OC=AB=3，OA=BC=4，∠COA=90°，求出OD=DE，根据勾股定理求出OA=AE=4，AC=5，在Rt△DEC中，根据勾股定理得出DE²+EC²=CD²，求出OD，即可得出答案．

解答 解：过D作DE⊥AC于E，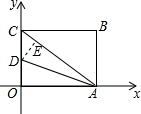
∵四边形ABCO是矩形，B（4，3），
∴OC=AB=3，OA=BC=4，∠COA=90°，
∵AD平分∠OAC，
∴OD=DE，
由勾股定理得：OA²=AD²-OD²，AE²=AD²-DE²，
∴OA=AE=4，
由勾股定理得：AC=$\sqrt{{3}^{2}+{4}^{2}}$=5，
在Rt△DEC中，DE²+EC²=CD²，
即OD²+（5-4）²=（3-OD）²，
解得：OD=$\frac{4}{3}$，
所以D的坐标为（0，$\frac{4}{3}$），
故答案为：（0，$\frac{4}{3}$）．

点评 本题考查了矩形的性质，角平分线性质，勾股定理的应用，能根据勾股定理得出关于OD的方程是解此题的关键．