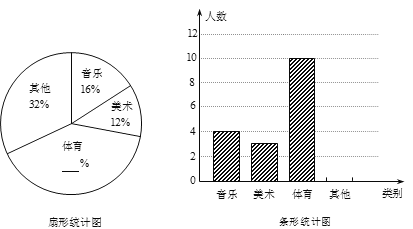
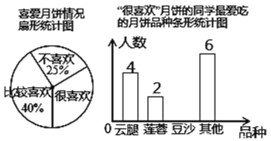
题目内容
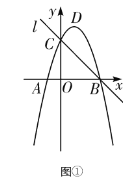
【题目】如图,已知抛物线![]() 与一直线相交于
与一直线相交于![]() ,
,![]() 两点.
两点.
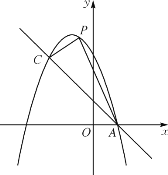
(1)求抛物线的函数表达式;
(2)求直线![]() 的函数表达式;
的函数表达式;
(3)若![]() 是抛物线上位于直线
是抛物线上位于直线![]() 上方的一个动点,求
上方的一个动点,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
【答案】(1)抛物线的函数表达式为![]() ;(2)直线
;(2)直线![]() 的函数表达式为
的函数表达式为![]() ;(3)
;(3)![]() 的面积最大值为
的面积最大值为![]() ;此时点
;此时点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)将![]() ,
,![]() 代入
代入![]() 即可求解;
即可求解;
(2)直接利用待定系数法即可求解;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的坐标为
的坐标为![]()
![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,得到
,得到![]() ,根据点
,根据点![]() 的坐标为
的坐标为![]() ,得到点
,得到点![]() 的坐标为
的坐标为![]() ,
,![]() ,进而得到
,进而得到![]()
 即可求解.
即可求解.
解:(1)将![]() ,
,![]() 代入
代入![]() ,得
,得
![]() 解得:
解得:![]()
∴抛物线的函数表达式为![]() .
.
(2)设直线![]() 的函数表达式为
的函数表达式为![]()
![]() ,将
,将![]() ,
,![]() 代入
代入![]() ,得
,得
![]() 解得:
解得:![]()
∴直线![]() 的函数表达式为
的函数表达式为![]() .
.
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,如图所示.
,如图所示.

设点![]() 的坐标为
的坐标为![]()
![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∵点![]() 的坐标为
的坐标为![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() ,∴
,∴![]() ,
,
∴![]()
![]()
 .
.
∵![]() ,
,
∴当![]() 时,
时,![]() 的面积取最大值,最大值为
的面积取最大值,最大值为![]() ;
;
此时点![]() 的坐标为
的坐标为![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】某学校为了了解九年级学生上学期间平均每天的睡眠情况,现从全校![]() 名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间
名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间![]() (单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
(单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
平均每天睡眠时间分组统计表
组别序号 | 睡眠时间 | 人数(频数) |
|
|
|
|
|
|
|
|
|
|
|
|
平均每天睡眠时间扇形统计表
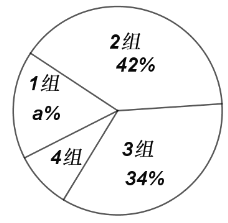
(1)![]() _______,
_______,![]() _______,
_______,![]() _______(
_______(![]() 为百分号前的数字);
为百分号前的数字);
(2)随机抽取的这部分学生平均每天睡眠时间的中位数落在_______组(填组别序号);
(3)估计全校![]() 名九年级学生中平均每天睡眠时间不低于
名九年级学生中平均每天睡眠时间不低于![]() 小时的学生有_______名;
小时的学生有_______名;
(4)若所抽查的睡眠时间![]() (小时)的
(小时)的![]() 名学生,其中
名学生,其中![]() 名男生和
名男生和![]() 名女生,现从这
名女生,现从这![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加个别访谈,请用列表或画树状图的方法求选取的
名学生参加个别访谈,请用列表或画树状图的方法求选取的![]() 名学生恰为
名学生恰为![]() 男
男![]() 女的概率.
女的概率.
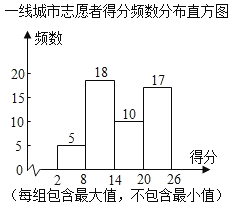
【题目】为了解疫情对精神负荷造成的影响,某机构分别在一线城市和三线城市的志愿者中随机选取了50人参加LES测试,根据志愿者的答题情况计算出LES得分,并对得分进行整理,描述和分析,部分信息如下:
一、三线城市志愿者得分统计表
城市 | 中位数 | 平均数 |
一线城市 | a | 17.6 |
三线城市 | 14 | 17.2 |
注:一线城市在14<x≤20中的得分是:15,15,16,17,17,17,17,18,18,20.
根据以上信息,解答下列问题:
(1)表中a的值为 ;
(2)得分越低反映个体承受的精神压力越小,排名越靠前,在这次调查中,一线城市的志愿者甲和三线城市的志愿者乙的得分均为15分,请判断甲、乙在各自城市选取的志愿者中得分排名谁更靠前,并说明理由;
(3)如果得分超过平均数就需要进行心理干预,请估计一线城市全部2000名志愿者中有多少人需要进行心理干预?