题目内容
 如图,MN是半圆O的半径,A是半圆的一个三等分点,B是
如图,MN是半圆O的半径,A是半圆的一个三等分点,B是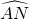 的中点,P是直径MN上的点,若AP+PB的最小值为
的中点,P是直径MN上的点,若AP+PB的最小值为 厘米,则圆的半径r=________厘米.
厘米,则圆的半径r=________厘米.
2
分析:作出点A关于MN的对称点A′,连接A′B,交MN于点P,则A′B为AP+PB的最小值,连接OA′,OB,易得∠BOA′=90°,
利用等腰直角三角形的性质可得半径的长.
解答:解 :作出点A关于MN的对称点A′,连接A′B,交MN于点P,则A′B为AP+PB的最小值,连接OA′,OB.
:作出点A关于MN的对称点A′,连接A′B,交MN于点P,则A′B为AP+PB的最小值,连接OA′,OB.
∴A′B=2 ,
,
∵A是半圆的一个三等分点,B是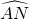 的中点,
的中点,
∴∠BON=30°,∠A′0N=60°,
∴△A′OB是等腰直角三角形,
∴OA′=2.
故答案为2.
点评:考查最短路线问题;若两点在直线的同一旁,则需作其中一点关于这条直线的对称点;作出整个圆的辅助性是解决本题的难点.
分析:作出点A关于MN的对称点A′,连接A′B,交MN于点P,则A′B为AP+PB的最小值,连接OA′,OB,易得∠BOA′=90°,
利用等腰直角三角形的性质可得半径的长.
解答:解
 :作出点A关于MN的对称点A′,连接A′B,交MN于点P,则A′B为AP+PB的最小值,连接OA′,OB.
:作出点A关于MN的对称点A′,连接A′B,交MN于点P,则A′B为AP+PB的最小值,连接OA′,OB.∴A′B=2
 ,
,∵A是半圆的一个三等分点,B是
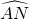 的中点,
的中点,∴∠BON=30°,∠A′0N=60°,
∴△A′OB是等腰直角三角形,
∴OA′=2.
故答案为2.
点评:考查最短路线问题;若两点在直线的同一旁,则需作其中一点关于这条直线的对称点;作出整个圆的辅助性是解决本题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,MN是半圆O的半径,A是半圆的一个三等分点,B是
如图,MN是半圆O的半径,A是半圆的一个三等分点,B是
 如图,MN是半圆O的直径,K是MN延长线上一点,直线KP交半圆于点Q,P.若∠K=20°,∠PMQ=40°,则∠MQP等于( )
如图,MN是半圆O的直径,K是MN延长线上一点,直线KP交半圆于点Q,P.若∠K=20°,∠PMQ=40°,则∠MQP等于( ) 的中点,P是直径MN上的点,若AP+PB的最小值为
的中点,P是直径MN上的点,若AP+PB的最小值为 厘米,则圆的半径r= 厘米.
厘米,则圆的半径r= 厘米.
 的中点,P是直径MN上的点,若AP+PB的最小值为
的中点,P是直径MN上的点,若AP+PB的最小值为 厘米,则圆的半径r= 厘米.
厘米,则圆的半径r= 厘米.