题目内容
所谓配方法其实就是逆用完全平方公式,即a2±2ab+b2=(a±b)2.该方法在数、式、方程等多方面应用非常广泛,如3+2 =12+2
=12+2 +(
+( )2;x2+2x+5=x2+2x+1+4=(x+1)2+4等等.请你用配方法解决以下问题:
)2;x2+2x+5=x2+2x+1+4=(x+1)2+4等等.请你用配方法解决以下问题:
(1)解方程:x2=5+2 ;(不能出现形如
;(不能出现形如 的双重二次根式)
的双重二次根式)
(2)若a2+4b2+c2﹣2a﹣8b+10c+30=0,解关于x的一元二次方程ax2﹣bx+c=0;
(3)求证:不论m为何值,解关于x的一元二次方程x2+(m﹣1)x+m﹣3=0总有两个不等实数根.
 =12+2
=12+2 +(
+( )2;x2+2x+5=x2+2x+1+4=(x+1)2+4等等.请你用配方法解决以下问题:
)2;x2+2x+5=x2+2x+1+4=(x+1)2+4等等.请你用配方法解决以下问题:(1)解方程:x2=5+2
 ;(不能出现形如
;(不能出现形如 的双重二次根式)
的双重二次根式)(2)若a2+4b2+c2﹣2a﹣8b+10c+30=0,解关于x的一元二次方程ax2﹣bx+c=0;
(3)求证:不论m为何值,解关于x的一元二次方程x2+(m﹣1)x+m﹣3=0总有两个不等实数根.
解:(1)x2=5+2 ,
,
x2=(
 )2,
)2,
x=±(
 );
);
(2)a2+4b2+c2﹣2a﹣8b+10c+30=0,(a﹣1)2+(2b﹣2)2+(c+5)2=0,
从而有a﹣1=0,2b﹣2=0,c+5=0,即a=1,b=1,c=﹣5,
∵ax2﹣bx+c=0,
∴x2﹣x﹣5=0
∴x= ;
;
(3)∵△=(m﹣1)2﹣4(m﹣3)=m2﹣6m+13=(m﹣3)2+4>0,
∴x2+(m﹣1)x+m﹣3=0总有两个不等实数根.
 ,
,x2=(

 )2,
)2,x=±(

 );
);(2)a2+4b2+c2﹣2a﹣8b+10c+30=0,(a﹣1)2+(2b﹣2)2+(c+5)2=0,
从而有a﹣1=0,2b﹣2=0,c+5=0,即a=1,b=1,c=﹣5,
∵ax2﹣bx+c=0,
∴x2﹣x﹣5=0
∴x=
 ;
;(3)∵△=(m﹣1)2﹣4(m﹣3)=m2﹣6m+13=(m﹣3)2+4>0,
∴x2+(m﹣1)x+m﹣3=0总有两个不等实数根.

练习册系列答案
相关题目
 .该方法在数、式、方程等多方面应用非常广泛,如
.该方法在数、式、方程等多方面应用非常广泛,如

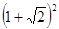 ;
;
 =
= 等等.请你用配方法解决以下问题:
等等.请你用配方法解决以下问题: ;(不能出现形如
;(不能出现形如 的双重二次根式)
的双重二次根式) ,解关于x的一元二次方程
,解关于x的一元二次方程 ;
; 总有两个不等实数根
总有两个不等实数根 .该方法在数、式、方程等多方面应用非常广泛,如
.该方法在数、式、方程等多方面应用非常广泛,如
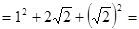
 ;
;
 =
= 等等.请你用配方法解决以下问题:
等等.请你用配方法解决以下问题: ;(不能出现形如
;(不能出现形如 的双重二次根式)
的双重二次根式) ,解关于x的一元二次方程
,解关于x的一元二次方程 ;
; 总有两个不等实数根
总有两个不等实数根 .该方法在数、式、方程等多方面应用非常广泛,如
.该方法在数、式、方程等多方面应用非常广泛,如

 ;
;
 =
= 等等.请你用配方法解决以下问题:
等等.请你用配方法解决以下问题: ;(不能出现形如
;(不能出现形如 的双重二次根式)
的双重二次根式) ,解关于x的一元二次方程
,解关于x的一元二次方程 ;
; 总有两个不等实数根
总有两个不等实数根