Question

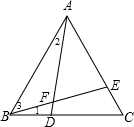
如图，等边△ABC，点D、E分别在BC、AC上，且BD=CE，AD与BE相交于点F．
（1）试求出∠AFE的度数．
（2）△AEF与△ABE相似吗？说说你的理由．
（3）BD²=AD•DF吗？请说明理由．

Answer 1

分析：（1）根据等边三角形的性质，可得AB=BC，∠ABC=∠C=∠BAC=60°，即可证明△ABD≌△BEC，即可以求得∠AFE=∠1+∠3=60°；
（2）根据∠AEF=∠AEB，∠AFE=∠BAE=60°，即可证明△AEF∽△ABE；
（3）易证△ABD∽△BFD，即可得

BD

AD

=

FD

BD

化简得BD²=AD•DF．

解答：解：（1）△ABC为等边三角形，
∴AB=BC，∠ABC=∠C=∠BAC=60°，
在△ABD和△BCE中

AB=BC ∠ABD=∠C BD=EC

，
∴△ABD≌△BCE（SAS），
∴∠1=∠2，
又∵∠AFE=∠2+∠3，
∴∠AFE=∠1+∠3=60°；

（2）在△AEF和△ABE中
∠AEF=∠AEB，∠AFE=∠BAE=60°，
∴△AEF∽△BEA；

（3）在△ABD和△BFD中，
∠BDF=∠ADB，∠1=∠2，
∴△ABD∽△BFD，
∴

BD

AD

=

FD

BD

，
∴BD²=AD•DF．

点评：本题考查了相似三角形的证明和相似三角形对应边比值相等的性质，考查了等边三角形各边长相等，各内角为60°的性质，本题中求证△ABD∽△BFD是解题的关键．