题目内容
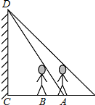
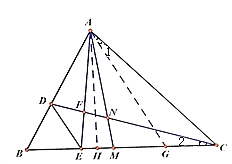
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上一点,
上一点,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
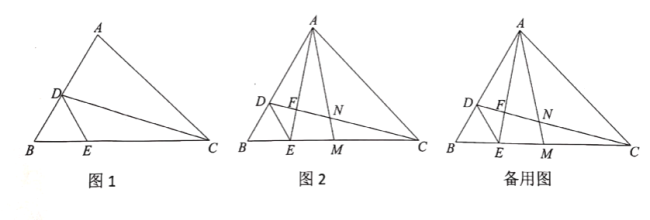
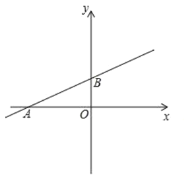
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
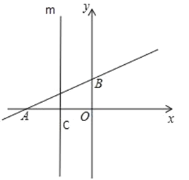
(2)如图2,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,直接写出线段
,直接写出线段![]() ,
,![]() ,
,![]() 的等量关系.
的等量关系.
【答案】(1)9-![]() (2)见解析(3)AD+MC= AC,理由见解析.
(2)见解析(3)AD+MC= AC,理由见解析.
【解析】
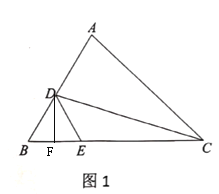
(1)过点D作DF⊥BE,根据等边三角形的的性质求出DF的长,再利用勾股定理求出CF,即可求出EC的长;
(2)作AG=AB, 得到△ABG为等边三角形,先证明△ABE≌△AGM,再证明△AGC≌△CED,得到CG=DE,再根据MG=BE=DE即可求解;
(3)作AH⊥BC,根据∠ACB=45°,∠BAC=75°,得到∠BAH=30°,∠HAC=45°设BH=x,
根据含30°的直角三角形与等腰直角三角形的性质分别表示出AD,MC,AC,即可求解.
(1)∵![]() ,
,![]() =
=![]()
∴△BDE为等边三角形,
作DF⊥BE,
∴EF=![]() BE=
BE=![]()
∴DF=![]()
∵CD=![]()
∴CF=![]() =9
=9
∴EC=CF-EF=9-![]() ;
;
(2)作AG=AB,∵∠B=60°,
∴△ABG为等边三角形,
∵AE=AM,∠ABE=∠AGM=60°,
∴△ABE≌△AGM,
∴∠ADC=60°+∠2=∠DAC=60°+∠1
故∠1=∠2,
∵∠AGC=120°=∠CED,AC=CD
∴△AGC≌△CED,
∴CG=DE,
又MG=BE=DE,
∴MC=MG+CG=2DE.
(3)∵∠ACB=45°,∠BAC=75°,
∴∠1=∠2=15°,
作AH⊥BC,∴∠BAH=30°,∠HAC=45°
设BH=x,
∴AB=2x,AH=![]() x=CH
x=CH
∴AC=![]() =
=![]() x,BC=(
x,BC=(![]() +1)x,
+1)x,
故CG=BC-BG=(![]() -1)x,BD=CG=(
-1)x,BD=CG=(![]() -1)x
-1)x
AD=AB-BD=(3-![]() )x
)x
CM=(2![]() -x)x
-x)x
∴AD+MC=(![]() +1)x=AC
+1)x=AC
即AD+MC= AC.

【题目】学校对初2021级甲、乙两班各60名学生进行知识测试(满分60分),测试完成后分别抽取了12份成绩,整理分析过程如下,请补充完整.
(收集数据)
甲班12名学生测试成绩统计如下:
45,59,60,38,57,53,52,58,60,50,43,49
乙班12名学生测试成绩统计如下:
35,55,46,39,54,47,43,57,42,59,60,47
(整理数据)
按如下分数段整理,描述这两组样本数据
组别频数 |
|
|
|
|
|
甲 | 0 | 1 | 3 | 3 | 5 |
乙 | 2 | 2 | 3 | 1 | 4 |
(分析数据)
两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 |
甲 |
| 52.5 | |
乙 | 48.7 | 47 |
|
(1)![]() ,
,![]() ;
;
(2)若规定得分在40分及以上为合格,请估计乙班60名学生中知识测试合格的学生有多少人?
(3)你认为哪个班的学生知识测试的整体水平较好,请说明一条理由.