题目内容
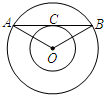 如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间满足的关系为
如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间满足的关系为R=2r
R=2r
.分析:首先连接OC,由大圆的弦AB切小圆于点C,根据切线的性质可得:OC⊥AB,又由∠AOB=120°,利用等腰三角形的三线合一的性质,可求得∠AOC=60°,然后利用三角函数,即可求得大圆半径R与小圆半径r之间满足的关系.
解答: 解:连接OC,
解:连接OC,
∵大圆的弦AB切小圆于点C,
∴OC⊥AB,
∵OA=OB,
∴∠AOC=
∠AOB=
×120°=60°,
在Rt△AOC中,cos∠AOC=
=
,
∴R=2r.
故答案为:R=2r.
 解:连接OC,
解:连接OC,∵大圆的弦AB切小圆于点C,
∴OC⊥AB,
∵OA=OB,
∴∠AOC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOC中,cos∠AOC=
| r |
| R |
| 1 |
| 2 |
∴R=2r.
故答案为:R=2r.
点评:此题考查了切线的性质、等腰三角形的性质以及三角函数的定义.此题比较简单,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 圆于点C,过点C作直线CE⊥AD,垂足为E,交大圆于F,H两点.
圆于点C,过点C作直线CE⊥AD,垂足为E,交大圆于F,H两点. 如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于P,如果AB=4cm,则图中阴影部分的面积为
如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于P,如果AB=4cm,则图中阴影部分的面积为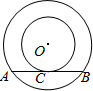 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,C为切点,若两圆的半径分别为3cm和5cm,则AB的长为
如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,C为切点,若两圆的半径分别为3cm和5cm,则AB的长为 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,切点为C,若AB=
如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,切点为C,若AB=