题目内容
18. 如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=6,BC=8,则DE的长为( )
如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=6,BC=8,则DE的长为( )| A. | 6.25 | B. | 6.35 | C. | 6.45 | D. | 6.55 |
分析 由翻转变换的性质得到∠EBD=∠CBD,根据平行线的性质得到∠EDB=∠CBD,得到EB=ED,设DE=x,根据勾股定理列方程,解方程即可.
解答 解:由翻转变换的性质可知,∠EBD=∠CBD,
∵AD∥BC,
∴∠EDB=∠CBD,
∴∠EDB=∠EBD,
∴EB=ED,
设DE=x,则BE=x,AE=8-x,
在Rt△ABE中,x2=62+(8-x)2,
解得,x=6.25,
故选:A.
点评 本题考查的是矩形的性质、翻转变换的性质,翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
8.下列四个图形中,是中心对称图形的是( )
| A. |  | B. |  | C. | 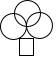 | D. | 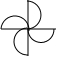 |
9.在下列所给出的坐标中,所表示的点在第一象限的是( )
| A. | (2,3) | B. | (-2,3) | C. | (-2,-3) | D. | (2,-3) |
13.已知:a=$\frac{1}{2-\sqrt{3}}$,b=$\frac{1}{2+\sqrt{3}}$,则a与b的关系是( )
| A. | 相等 | B. | 互为相反数 | C. | 互为倒数 | D. | 平方相等 |
7. 如图,已知∠ABC=∠DCB,添加下列条件,△ABC与△DCB不能全等是( )
如图,已知∠ABC=∠DCB,添加下列条件,△ABC与△DCB不能全等是( )
 如图,已知∠ABC=∠DCB,添加下列条件,△ABC与△DCB不能全等是( )
如图,已知∠ABC=∠DCB,添加下列条件,△ABC与△DCB不能全等是( )| A. | AC=DB | B. | AB=DC | C. | ∠A=∠D | D. | ∠1=∠2 |
8.已知点A(3,-2)、B(1,-2),则直线AB( )
| A. | 与x轴垂直 | B. | 与x轴平行 | C. | 与y轴重合 | D. | 与x、y轴相交 |