题目内容
已知：如图，∠A=33°，∠B=83°，∠ADC=146°，求∠C的度数．
解：延长AD交BC于点E，
∵∠AEC是△ABE的一个外角，
∴∠AEC=∠A+∠B=33°+83°=116°．
∵∠ADC是△DEC的一个外角，
∴∠C=∠ADC-∠AEC=146°-116°=30°．
分析：延长AD交BC于点E，根据三角形的外角等于与它不相邻的两个内角之和可求∠C的度数．
点评：本题主要考查了三角形外角的性质，解题关键是正确作出辅助线．
∵∠AEC是△ABE的一个外角，
∴∠AEC=∠A+∠B=33°+83°=116°．
∵∠ADC是△DEC的一个外角，
∴∠C=∠ADC-∠AEC=146°-116°=30°．
分析：延长AD交BC于点E，根据三角形的外角等于与它不相邻的两个内角之和可求∠C的度数．
点评：本题主要考查了三角形外角的性质，解题关键是正确作出辅助线．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，测得C在B的北偏西45°方向上．
11、已知，如图，正比例函数与反比例函数的图象相交于A、B两点，A点坐标为（2，1），分别以A、B为圆心的圆与x轴相切，则图中两个阴影部分面积的和为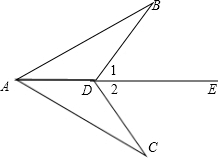
已知，如图，∠1=∠2，
已知，如图，直角坐标系内的矩形ABCD，顶点A的坐标为（0，3），BC=2AB，P为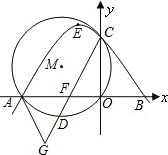
于C点，⊙M经过原点O及点A、C，点D是劣弧