题目内容
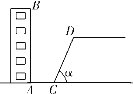
【题目】如图,在平面直角坐标系中,直线y=![]() x+15分别交x轴、y轴于点A,B,交直线y=
x+15分别交x轴、y轴于点A,B,交直线y=![]() x于点M.动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒.
x于点M.动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒.
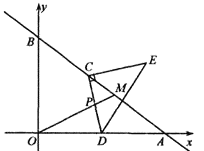
(1)求点A的坐标和AM的长.
(2)当t=5时,线段CD交OM于点P,且PC=PD,求a的值.
(3)在点C的整个运动过程中,
①直接用含t的代数式表示点C的坐标.
②利用(2)的结论,以C为直角顶点作等腰直角△CDE(点C,D,E按逆时针顺序排列),当OM与△CDE的一边平行时,求所有满足条件的t的值.
【答案】(1)A(20,0),10;(2)2;(3)①![]() ,②
,②![]() 或
或![]() 或4
或4
【解析】
(1)在![]() 中,令
中,令![]() ,得点A坐标,联立AB,OM解析式,求出点M坐标,过点M作
,得点A坐标,联立AB,OM解析式,求出点M坐标,过点M作![]() 轴垂线,垂足为G,由M坐标得出OG,MG,AG长度,由勾股定理可得结果.
轴垂线,垂足为G,由M坐标得出OG,MG,AG长度,由勾股定理可得结果.
(2)过点C作CQ![]()
![]() 轴交OM延长线与Q,证明△CPQ≌△DPO(AAS),得出CQ=OD,解出CQ长度即可.
轴交OM延长线与Q,证明△CPQ≌△DPO(AAS),得出CQ=OD,解出CQ长度即可.
(3)①作CK![]()
![]() 轴与K,由CK
轴与K,由CK![]()
![]() 轴,得
轴,得![]() ,解出
,解出![]() CK,代入
CK,代入![]() 中,得
中,得![]() .
.
②当OM![]() 于△CDE的一边,分三种情况进行讨论:当OM
于△CDE的一边,分三种情况进行讨论:当OM![]() CD 时,用
CD 时,用![]() 解得t值;当OM
解得t值;当OM![]() CE时,用CK=2DK解得t值;当OM
CE时,用CK=2DK解得t值;当OM![]() DE时,证明△CDK≌△CEG,用DH=2EH解得t值.
DE时,证明△CDK≌△CEG,用DH=2EH解得t值.
解:(1)当y=0时,![]() ,解得:x=20
,解得:x=20
∴点A(20,0);
∵两直线相交于点M
∴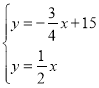 ,解得:
,解得:![]()
∴点M(12,6)
过点M作MG⊥OA于点G

∴OG=12,MG=6
∴AG=20-12=8
在Rt△AMG中,
![]() ;
;
(2)∵动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒![]() 个单位的速度从点0沿OA的方向运动,
个单位的速度从点0沿OA的方向运动,
∴当t=5时则AC=15,OD=5![]() ,AB=25
,AB=25
点C(8,9)
过点C作CQ∥x轴交OM的延长线于点Q,
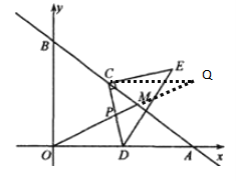
∴点Q(18,9)
∴CQ=18-8=10,
∵CQ∥x轴
∴∠G=∠DOP
在△CPQ和△DPO中,

∴△CPQ≌△DPO(AAS)
∴CQ=OD
即5![]() =10,解之:
=10,解之:![]() =2.
=2.
(3)解:①过点C作CK⊥x轴于点K,
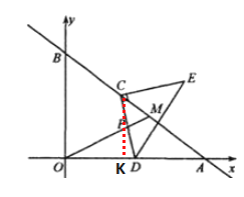
由题意可知AC=3t,AB=25,OB=15,
∴CK∥y轴,
∴△ACK∽△ABO
∴![]() 即
即![]()
解之:![]()
当![]() 时,则
时,则![]()
解之:![]()
∴点![]() ;
;
②由①可知CK=![]() , OK=
, OK=![]()
∵AC=3t,OD=2t,tan∠MOA=![]()
当CD∥OM时,

![]() 即
即![]()
解之:t=![]() ;
;
当CE∥OM时,

∴∠ECD=∠CPO=90°
∴∠DCK+∠CDK=∠DOP+∠CDK=90°
∴∠DCK=∠DOP
∴tan∠DCK=![]()
∴CK=2DK
∴DK=OD-OK=![]()
∴![]()
解之:![]() ;
;
当DE∥OM时,过点E作EH⊥x轴于点H,过点C作CK⊥x轴于点K,过点C作CG∥x轴交HE于点G,
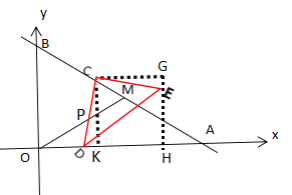
∵等腰直角△CDE
∴CD=CE
易证△CDK≌△CEG,
∴CK=CG=GH=![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
∵OM∥ED,
∴∠MOA=∠EDH,![]()
∴DH=2EH
∴![]()
解之:t=4.
∴t的值为![]() 或
或![]() 或4.
或4.